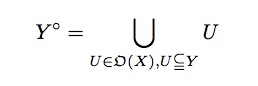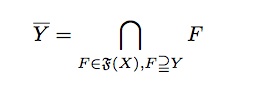学んでみよう！記号論理

高崎金久著，日本評論社 2014年8月刊行．A5判，224頁，2700円，ISBN978-4-535-78760-5． [概要, 目次, 訂正]

概要

2000年頃，私は所属する大学で学部学生向けの数理論理学の講義を担当することになり，それまでほとんど知識のなかった記号論理を一から学んで講義を始めた．それ以来，途中で2年間ほど休んだとき以外は，毎年この講義を行ってきた．この講義の中では，何よりもまず記号化の意味を理解させること，そして記号化された論理を通じて数学の命題や証明について考えさせることを重視した．そのために，数学の論証の形式に近い「自然演繹」を演繹体系として採用した．さらに，数理論理学では記号化された証明を「証明図」あるいは「導出図」と呼ばれる図で表すことが多いが，この講義では記号化された証明のさまざまな例を選び，それらを数学の証明のようにあえて1行1書き下すこと（一種の疑似数学的作業）を行った．

本書は雑誌『数学セミナー』でこの講義の内容を紹介した連載記事「記号論理の手習い」（2012年10月号〜2013年12月号）に加筆修正を行ったものである．時間的制約から講義では立ち入ることのできない重要な話題としてタブロー法，ハイティング代数，ヘンキンの定理の証明なども紹介し，随所にやや暴走気味の小ネタを挿入したりしたので，内容的にはかなり濃いものになった．さらに，講義用の教科書や参考書として利用されることを想定して，巻末に数学的予備知識の解説や本文中の練習問題の略解（詳解を書いてしまうと演習やレポートの問題として使いにくいので，適当に省略している）を書き加えた．

第1講　論理の記号化
　　1. 数理論理学とは何だろうか
　　2. 命題
　　3. 述語
　　4. 推論
第2講　命題論理の考え方
　　1. 論理パズル
　　2. 論理式への翻訳
　　3. 真理値と論理計算
　　4. 真理値による論理結合子の解釈
　　5. 真理値割り当てによる論理式の解釈
　　6. まとめ
第3講　意味論的諸概念
　　1. 論理式の同値性
　　2. 論理式の同値変形
　　3. 論理式の恒真性
　　4. 意味論的帰結
　　5. まとめ
第4講　論理式の標準形
　　1. 論理和標準形（DNF）
　　2. 充足問題との関係
　　3. 論理積標準形（CNF）
　　4. 恒真性との関係
　　5. まとめ
第5講　タブロー法
　　1. タブローの意味論的見方
　　2. タブローの構文論的見方
　　3. 充足可能性や恒真性の判定
　　4. 意味論的帰結の判定
　　5. まとめ
第6講　命題論理の演繹体系
　　1. 演繹体系についての基本的な概念
　　2. ヒルベルト流の演繹体系
　　3. 形式的証明の例
　　4. 基本的定理
　　5. ゲンツェン流の演繹体系
　　6. まとめ
第7講　命題論理の自然演繹(1)
　　1. 演繹体系の設定
　　2. ∧，∨に関する推論規則
　　3. ∧，∨に関する形式的証明の例
　　4. →，⇔関する推論規則と形式的証明の例
　　5. まとめ
第8講　命題論理の自然演繹(2)
　　1. ¬，⊥に関する推論規則
　　2. 形式的証明の例
　　3. 派生的推論規則
　　4. NKの別の形式化
　　5. まとめ
第9講　命題論理の自然演繹(3)
　　1. ブール代数とハイティング代数
　　2. 束論における見方
　　3. 直観主義論理の意味論
　　4. 直観主義論理の演繹体系
　　5. まとめ
第10講　述語論理の考え方
　　1. 述語論理の論理式
　　2. 言葉から論理式への翻訳
　　3. 閉論理式
　　4. 等号公理と等号推論
　　5. まとめ
第11講　述語論理の意味論
　　1. 意味論の舞台設定
　　2. 充足関係
　　3. 論理式の同値性
　　4. 論理式の恒真性
　　5. まとめ
第12講　述語論理の演繹体系
　　1. 述語論理の自然演繹
　　2. 量化記号に関する推論規則
　　3. 形式的証明の例
　　4. その他の演繹体系
　　5. まとめ
第13講　完全性定理(1)
　　1. 完全性定理の定式化
　　2. 完全性定理の直接的証明
　　3. 補助定理の証明
　　4. まとめ
第14講　完全性定理(2)
　　1. ヘンキンの定理と完全性定理
　　2. 極大無矛盾な論理式集合
　　3. ヘンキンの定理の証明
　　4. コンパクト性定理
　　5. まとめ
第15講　完全性定理(3)
　　1. 述語論理におけるヘンキンの定理
　　2. ヘンキン性と極大無矛盾性
　　3. 極大無矛盾でヘンキン性をもつ閉論理式集合のモデル
　　4. ヘンキンの定理の証明
　　5. まとめ
付録　数学的予備知識
　　1. 集合
　　2. 写像
　　3. 関係
　　4. 演算
　　5. 位相
　　6. 帰納法

訂正

注意：以下ではHTMLで書くのが難しい表現を代替表示しています．（例）a に上線をつけたものは a^-，波線をつけたものは a^~で代用しています．

p.82, 例2：3行目「]⁷」→「]⁶」
5行目「(2,5 ¬E)」→「(2, 4¬E)
6行目「(4-6 ¬I)」→「(3-5 ¬I)」
p.84, 例6：7行目「(5 ∨I)」→「(6 ∨I)」
p.86, 上から7行目：「¬除去」→「¬導入」
p.87, 下から3行目：「次のことをを意味」→「次のことを意味」
p.93, 脚注2)：「この連載」→「本書」
p.95, 中段：有界束の定義において 1 ≠ 0 も条件として加える必要がある．
p.126, 中段：D = {a,b} については a ≠ b を想定している．
p.137, 例3の解説：
- 5行目：「新たに導入された変数 a に対してP(a)→Q(a)を導いて」→ 「新たに導入された変数 a に対してP(a)→R(a)を導いて」
- 6〜7行目：「P(a)→Q(a)を導くにはP(a)を仮定してQ(a)を導けばよい」→ 「P(a)→R(a)を導くにはP(a)を仮定してR(a)を導けばよい」
- 9行目：「目標のQ(a)を導く」→「目標のR(a)を導く」
- 11行目：「P(a)→Q(a)を導く」→「P(a)→R(a)を導く」
p.138, 例5の前半5行目：「∀E」→「∧E」
p.161, 脚注1)：「加算」→「可算」
p.175, 下から10行目：「加算」→「可算」
p.177, 下から11行目：「加算」→「可算」
p.184, 下から1行目：右端の ∩の下の式「λ∈λ」→「λ∈Λ」．ちなみに，ここで考えるΛは空集合と異なるとする．
p.186, 中段：Yの開核と閉包の定義式が間違っている．正しくは以下の通り：
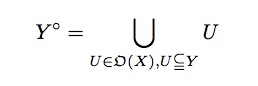
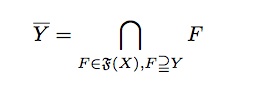
p.190, 第3講練習問題3の略解：「(19), (30), (31)は」 →「(29), (30), (31)は」
p.193, 第6講練習問題３の略解：「…を仮定する． Γ|-φ→(ψ₁→ψ₁)の証明」 →「…を仮定する．「 Γ|-φ→ψ₁の証明」

なお，第15章の完全性定理の証明では陰に選択公理を用いているが，本書（連載）の入門的な性格に鑑みて，そのことはあえて明言しなかった．また，述語記号として等号が存在する場合には，この完全性定理の証明は修正を要する．これらのことについては，角田譲『数理論理学』（参考文献[5]）の第2章2.4節を参照されたい．