理科系の数学入門 (斎藤秀司・三松佳彦・戸瀬信之編)

第4巻 常微分方程式

微分方程式は未知関数とその導関数の関係を 方程式にしたものである．常微分方程式の起源は 物理学，特に力学の研究にある．力学には大別して， 力が拮抗して静止した状態を扱う静力学と， 物体の運動を扱う動力学がある．動力学の基本法則は 17世紀にニュートンによって見出された． それは物体の加速度と物体に働く力の比例関係を表す ものであり，物体の座標を時間の関数と見なすとき， ２階までの導関数を含む常微分方程式になる． ただし，ニュートンの時代には微積分学が まだ発展途上にあり，微分方程式が力学の基礎として 用いられるようになったのは18世紀である（同時に 微積分学が解析学に進化した）．さらに時代が下って， 19世紀に電気・磁気・熱現象が研究対象になると， 時間と空間の両方に関する物理量の変化の法則を 書き下すために偏微分方程式も用いられるようになった．

今日では，理工系の学問を学ぶ人にとって（程度の差は あっても）微分方程式に関する知識は必要不可欠である． さらに，近年は経済学においても微分方程式の重要性が 高まっている．もちろん，純粋に数学的な観点から見ても， 微分方程式は重要かつ興味深いものであり，解析学の中で 中心的な位置を占めている．

本書は初めて常微分方程式を学ぶ人のために書かれた入門書である． 予備知識としては大学１年で学ぶ程度の微積分学と線形代数を 仮定するが，必要に応じて重要事項の復習や補足説明を行っている．

1章は本書全体の導入部である．前半で微分方程式が 方程式としてどのような意味や解釈をもつものであるかを 簡単に説明した後，後半では，物理学や生物学に登場する 微分方程式の例を通じて，「数理モデル」としての 微分方程式の使い方を解説している．また，後の章で扱う 基本的な概念や方法の一端もここで紹介している．

2章〜4章は「解ける」（正確に言えば「求積」可能な） 微分方程式を扱う．従来の入門書では，このような 微分方程式は体系的な考察の対象とは見なされず， さまざまな例の羅列として扱われることが多かった． 本書では，「第１積分」という概念を軸にして， これらを可能な限り統一的に扱っている． これは「可積分系」と呼ばれる微分方程式の研究分野の 基本的な考え方に沿ったやり方である．これによって， １階微分方程式のいわゆる「初等解法」から， やや難解な「完全微分型」の方程式の話題を経て， 力学の「解ける」運動方程式に至るまでの道のりを ごく自然にたどることができるのである．

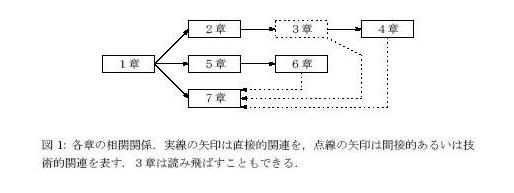
さらに3章では，この道中の寄り道として，ベクトル解析・ 微分形式や調和関数・共役調和関数・正則関数などにも触れている． 先を急ぐ読者はこの部分を読み飛ばして先に進むこともできるが， 余裕がある読者はこの題材を通じて，常微分方程式と 数学の他の話題との意外な関連の一端を見ていただきたい．

5章〜6章では線形微分方程式を扱う．線形微分方程式は 常微分方程式の教科書の定番の話題であり，工夫の余地が 少ないように思われるので，ごく標準的な内容にとどめている． 線形微分方程式の鍵は「線形性」（線形代数の「線形」と同じ） にある．それによって問題を「基本解」と呼ばれる文字どおり 基本的な解を求めることに帰着できる．特に「定数係数の方程式」 と呼ばれるものは「求積」とは別の意味で「解ける」方程式であり， 基本解などを具体的に求めることができる．このような 線形微分方程式の取り扱いの知識は理工系のどの分野でも 必要な常識中の常識である．

7章では一般的な微分方程式を扱う．2章〜6章で扱ったような 「解ける」微分方程式では，解を具体的に書き下すことができる． それができない一般の方程式にどのように立ち向かうか， というのがこの章のテーマである．前半では， そもそも解は存在するのか，という問題を考える． この問に対する答が「初期値問題の解の存在と一意性の定理」 である．後半では，微分方程式を「相空間」という幾何学的な 設定の中で見直す「定性的理論」の入り口の部分を紹介する． この章の内容は他の章よりも高度で理論的なものなので， 細かいことにこだわらず，発展的な話題として気楽に 読んでいただきたい．

第1章 微分方程式とは何か

1.1 微分方程式とその解

1.2 正規形の微分方程式とその意味

1.3 数理モデルとしての微分方程式

1.4 例：指数法則の方程式

1.5 例：自由落下の方程式

1.6 例：生物種の相互作用の方程式

第2章 求積可能な１階微分方程式

2.1 求積とは何か

2.2 変数分離型の方程式

2.3 線形微分方程式

2.4 変数分離型や線形微分方程式に帰着する方程式

2.5 完全微分型の方程式

2.6 完全微分型であるための条件

第3章 積分可能条件とその応用

3.1 微分形式

3.2 全微分方程式

3.3 調和関数・共役調和関数・正則関数

第4章 求積可能な力学の方程式

4.1 保存力を受ける物体の運動方程式

4.2 例：正弦振動の運動方程式

4.3 例：線形斥力のもとでの運動方程式

4.4 例：振り子の運動方程式

4.5 相空間上の力学系としての見方

第5章 線形微分方程式

5.1 線形微分方程式の一般的性質

5.2 定数係数線形微分方程式の基本解系

5.3 非同次方程式と定数変化法

5.4 定数係数の場合の非同次方程式

第6章 線形連立１階系

6.1 線形連立１階系の一般的性質

6.2 定数係数線形連立１階系の基本解行列

第7章 一般的な微分方程式

7.1 初期値問題の解の存在と一意性

7.2 ２次元相空間上の定性的解析

参考文献

練習問題の解答・ヒント

• p.11, 11行：2つの式の右辺にhを掛け忘れている． 「f(jh,y_j,z_j)」 →「f(jh,y_j,z_j)h」， 「g(jh,y_j,z_j)」 →「g(jh,y_j,z_j)h」，
• p.27, 7行： 右辺の「-g - ag」→「-aw - g」
• p.27, 図1.13：縦軸の左側の「-w_∞」→「w_∞」
• p.29, 9行: dx/dt, dy/dt が「同符号をとる」と書いたが， これでは「ともに正またはともに負」という意味に誤解されてしまう． 「一定符号をとる」と書くべきだった．
• p.36, 8行〜9行：f(x), F(x) の符号が間違っている． f(x) = 1/x, F(x) = log|x| が正しい．
• p.40, 下から7行：「同時方程式」→「同次方程式」
• p.42, 7行：u₁(x) と u₂(x) を入れ換える．
• p.43, (2.10)式：左側の式の「 (x,t)」 →「 (x,y)」
• p.48, (2.15)式：右辺第2項「f(x,y~)」→「(x,y~))」
• p.55, (2.15)式：右辺の２つの積分の dx^~ と dy^~ を入れ換える．すなわち最初の積分は x^~ に関する積分，次の積分は y^~ に関する積分である．
• p.72, 8行：「dx=」の右辺→「u_z(z,w)dz+u_w(z,w)dw」， 「dy=」の右辺→「v_z(z,w)dz+v_w(z,w)dw」，
• p.72, 10行：「dv(u,v)」→「dv(z,w)」
• p.72, 12行：「u_x(x,y)」→「u_z(z,w)」， 「u_y(x,y)」→「u_w(z,w)」， 「v_x(x,y)」→「v_z(z,w)」， 「v_y(x,y)」→「v_w(z,w)」，
• p.75, 最後の式：fをすべてgに置き換える．
• p.76, 最初の式：gをすべてfに置き換える．
• p.87, 6行：右辺の各項の符号を逆にする．
• p.88, 下から1行：中辺および右辺の各項の符号を逆にする．
• p.89, 1行：右辺の各項の符号を逆にする．
• p.91, 10行，17行：右辺の符号を逆にする．
• p.109, 最後の２式：両式の左辺「dx」→「√m dx」， 最後の式の右辺の 1/a の分子「1」→「√m」
• p.110, 1行：1/a の分子「1」→「√m」
• p.110, 3行：右辺第2項の a/2 の分母「2」→「2m」
• p.117, 図4.6：右側のグラフは arccosh そのものではなくて (4.14) の関数のグラフである．右半分 (t ≧ 1 の部分)が arccosh のグラフになる．
• p.130, 下から3行：「(x,y) = (x(x), y(t))」→「(x,y) = (x(t), y(t))」
• p.158, 下から6行：「x ^k」→「x ^j」
• p.169, (5.15)式：右辺第2項「f⁽ⁿ⁾(x)g(x)」 →「Σ_j=1ⁿ C_ju_j(x)」
• p.185, 第2式：右辺の行列の (2,n) 成分「a_1n」→「a_2n」
• p.225, 下から1行：「a)」→「i)」，「b)」→「ii)」
• p.257, 5行：ベクトルの第２成分の e^axの「ax」→「α₁x」