この章からしばらくは古典論理の意味論を紹介する. その導入部として,この章では命題論理の論理式の概念と 真理値による意味解釈の方法を扱う.前半ではパズルや 論理回路を例に選んで記号化の考え方を説明する.後半では, 論理式の構文や意味解釈をきちんと定式化し,それに基づいて 「同値性」,「恒真性」,「充足関係」,「モデル」などの 基本的概念を導入する.同値式や恒真式の基本的な例も示す.
この言葉遣いは普通の数学での慣用とはかなり違うことに 注意されたい.数学ではひとまとまりの言明を内容の重みや 説明のなかの位置づけに応じて命題・定理・系・補題などと 呼ぶ.論理学の考え方に従えばこれらはすべて「定理」, すなわち証明された言明(従ってすべて真)である.
なお,ここでは命題の内容そのものに立ち入る必要はないから, 「箱」と「ボール」を「子供」と「帽子」に置き換えて 「子供と帽子」のパズルにしても同じことである.実際,
パズルでは一連の条件を与えてそれを満足する状況 (ボールの入れ方)を見つけることを問う.条件は 命題変数を「論理演算子」(「真」と「偽」 の値に対する論理演算をあらわす)で組み合わせた 「論理式」の形に表わすことができる. 条件を論理式の形で表現すれば,パズルはその論理式が 真となるような命題変数の値の割り当て方を見つける 問題に帰着する.これは「充足問題」と呼ばれる 問題であり,解法が知られている.
情報科学の視点から見れば,命題とは「ビット」 に他ならない.ビットとは要するに,二つの状態だけを とり得るような量のことである.通常,この二つの状態 を 0 と 1 で表わすことが多い.これらを
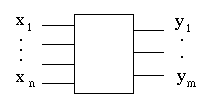
このようなビットを入出力する回路を「論理回路」と いう.論理回路は図式的に

実はこのようなブール函数は,x1,..., xn を命題変数とみなせば,命題論理の論理式 として必ず書ける(これは次の章で示す).命題論理は このように論理回路やその動作を抽象化したものと考える こともできる.
n 個の命題変数 x1, ..., xn があれば, 全部で 2n 通りの真理値の組み合わせが生じる.
| 論理演算子 | 種別 | 使い方 | 意味 |
|---|---|---|---|
| 連言∧ | 2項演算 | P∧Q | PかつQ |
| 選言∨ | 2項演算 | P∨Q | PまたはQ |
| 否定¬ | 1項演算 | ¬P | Pでない |
| 含意→ | 2項演算 | P→Q | PならばQ |
| 同値↔ | 2項演算 | P↔Q | PはQと同値である |
この定義を次のような表(「真理表」)の 形で示すことも多い:
| p | q | p∧q | p∨q | p→q | p↔q |
|---|---|---|---|---|---|
| T | T | T | T | T | T |
| T | F | F | T | F | F |
| F | T | F | T | T | F |
| F | F | F | F | T | T |
| p | ¬p |
|---|---|
| T | F |
| F | T |
実はこれは2個の要素からなるブール代数 {T, F} を考えていることに他ならない. これによって連言∧と選言∨はブール代数の演算∧, ∨に対応する. また否定¬p はブール代数での補要素 x'に対応する.
が成り立つからである.数学では否定命題をつくることが 多い --- たとえば対偶や背理法を考えてみよ --- から, 否定命題が機械的につくれる方が都合がよいのである.
たとえば,数学の定理は「Pならば(前提)Qである(帰結)」 という形をとることが多いが,前提Pが満たされなければ この定理はもちろん使われない.しかしそれは定理が 正しくないという意味ではなく,単に無内容なだけである. 「定理」は前提の如何によらず真であるべきだから, 前提が偽の場合には定理自体を機械的に真にしておけばよい. これが p = F のときに q によらず p→q = T とする理由である.
また,→をこのように定義しておくと,p, q の値によらず
が成り立つ.対偶命題に言い替えて考えることも数学では よく行うので,それが同値である方が都合がよいことは 間違いない.
ちなみに,右辺に現れているものはすべて命題論理の 論理式の例でもある.左辺ももちろん論理式である (論理式についてはこのあとで詳しく説明する).
命題論理の論理式を構成するのは次のような記号である.
これらを用いて以下のように定義されるものを「論理式」という.
【注意】このように,原子的なものから出発し, すでに得られたものから新たなものを生成する規則を与える ことで全体を定義する,という定義の仕方を 「帰納的定義」(あるいは「再帰的定義」) という.これは有限の言葉で無限の対象を定義するやり方 であり,離散数学・数理論理学・計算機科学のさまざまな 場面で用いられる.これによって数学的帰納法が使いやすく なるという利点もある.
【例】(p→(q∧r))∨((¬p)→s)), ((¬(¬p))→p) などは論理式である.(p∧(∨q)) は論理式でない(構文が 正しくない).
同じことは数式についても行われるので,まずそちらに ついて説明する.数式では乗算・除算は加算・減算よりも 優先順位が高いものと解釈される.したがって, (((a + b) * c) + (d * e)) は (a + b) * c + d * e というように省略できる. この中の (a + b) の括弧は a + b を優先して行う ためのものなので省略できない.
論理式の場合は,¬が最も優先順位が高く,その次は ∧と∨で,→と↔は最も優先順位が低いとみなす, というのが普通のやり方である.これに従えば, (p→(q∧r))∨((¬p)→s)), ((¬(¬p))→p) は それぞれ (p→q∧r)∨(¬p→s), ¬¬p→p というように 表せる.これ以上括弧を省略すると意味が違って来る.
同じ論理結合子のみが繰り返し現れるときには括弧を省略する. たとえば,((..(φ1∧φ2)∧φ3∧) …∧φn) は φ1∧φ2∧φ3∧ …∧φn と略記する.∨についても同様である.
さらに,たとえば p→q→r を p→(q→r) の略記法として 用いる記法もあるが,これはここでは採用しない.
| x1 | x2 | ・・・ | xn |
|---|---|---|---|
真理値割り当て M の下での命題変数 xi の値を M[xi] と表わす.
真理値割り当てを与えることは添字集合 I の部分集合を 与えることと同じである,ということに注意されたい. 実際,真理値割り当て M に対して
という I の部分集合(要するに上の表で T が入る変数の
添字を集めたもの)を対応させると,これは1対1の対応になる.
論理式φに含まれる変数が x1,
..., xn であるとする.これらの
真理値割り当て M が与えられれば φ の真理値が定まる.
これを真理値割り当て M の下での論理式φの「解釈」
という.真理表の一つの行
は命題変数の真理値割り当てとその下での論理式の値を
並べて書いたものということになる.
これをもう少し形式張って定式化し直すと,
次のような帰納的な定義になる.
【定義】
命題変数 x1, ..., xn の真理値割り当て M が
与えられたとする.x1, ..., xn から
構成される各論理式φに対して,真理値割り当て M の下での論理式φ
の解釈 M[φ] を次のように帰納的に定める:
【演習問題】p,q,r のすべての真理値割り当てに対して論理式
φ = p→(q→r) の真理値を求めよ.
【定義】論理式φ, ψが論理的に同値である
(あるいは単に,同値である,ともいう)とは,
φ, ψに含まれる命題変数のあらゆる真理値割り当て M に対して
M[φ] = M[ψ] となることをいう.φ, ψが論理的に同値
であることを記号的に φ≡ψ と表わす.
【例】論理結合子の間の関係
【例】任意の論理式φ, ψに対して
たとえば,ド・モルガンの法則(最初のもの)は次の真理表の
¬(φ∨ψ) と ¬φ∧¬ψ の列を見比べることで確かめられる.
【演習問題】他の関係も同様にして確かめよ.
いずれも基本的かつ重要な関係である.
≡と↔を混同しないように注意されたい.
前者は論理式の間の関係を表わすものであり,
後者は論理式の構成要素である.もっとも,
次の項で注意するように,両者は無関係ではない.
【定義】論理式φに含まれる命題変数のあらゆる
真理値割り当て M に対して常に M[φ] = T となるとき,
φは恒真式であると言って,
記号的に |= φ と表わす.同様に,
任意の真理値割り当て M に対して常に M[φ] = F となるとき,
φは恒偽式であると言う.
【注意】
【例】任意の論理式 φ, ψ, χ に対して
たとえばmodus ponensは次のように真理表で確かめられる:
【演習問題】同様にして他の論理式の恒真性も確かめよ.
いずれも基本的かつ重要な恒真式である.
この問題の解決法も普通の数学と同様である.すなわち,
いろいろな公式(たとえば,上に示したような分配律や
ド・モルガンの法則などの基本的な同値関係)を用いて
論理式を同値変形するのである.このことは正確には
次のように定式化される:
【定義】ψ が論理式φの中に含まれる一連の文字列で
それ自体が論理式であるとき,ψはφの部分論理式
であるという.
【例】¬(c∧d) は (a∧b)→¬(c∧d) の部分論理式である.
【定理】ψがφの部分論理式であるとする.またψ'はψと
同値な論理式である(つまり ψ≡ψ')とする.このとき
φの中でψが現れる部分を一つ選んでそれをψ'で置き換えて
得られる論理式φ'はφと同値である.
【例】上の例を考える.ド・モルガンの法則により
¬(c∧d) ≡ ¬c∨¬d だから
である.さらに→の別表現を用いれば
【定義】論理式φが真理値割り当て M に対して真(M[φ] = T)であるとき,
真理値割り当て M は論理式φを充足する(あるいは
真理値割り当て M は論理式φのモデルである)と言う.
真理値割り当て M と論理式φのこの関係を記号的に
と表わす.さらに,この関係を真理値割り当て M と論理式の集合Γ
に拡張して考えることもできる.すなわち,
Γに属する任意の論理式φに対して M |=φ であるとき,
真理値割り当て M は論理式の集合Γを充足するあるいは
真理値割り当て M は論理式の集合Γのモデルであると言って
と表わす.Γが有限個の論理式φ1,…,φn
からなるときにはこれは
M |= φ1∧…∧φn と同じことである.
論理式あるいは論理式の集合がモデルをもつとき
充足可能であるという.
【例】「箱とボールのパズル」は与えられた条件を
表わす論理式φに対してそれを充足するような真理値割り当て M
(すなわちボールの入れ方)を求める問題として
定式化される.たとえばφ= (a∧b→¬c)∧(¬a→b∨c)
という論理式は
これまでたびたび言及してきた「充足問題」とは,
与えられた論理式φを充足するような真理値割り当て(つまりモデル)
を求める問題のことである.次章で説明する論理式の
「標準形」は充足問題の解法も与える.
【定義】論理式の集合Γと論理式ψに対して,
Γを充足する任意の真理値割り当て M がψも充足すること
(すなわち M |=Γ ならば M |=ψ となること)を
と表わし,意味論的演繹関係と呼ぶ.
これは「Γが正しければψも正しい」ということを意味している.
論理式ψが恒真であることを |= ψ と表わす理由もこれで明らかになる.
実際,|= ψ では前提は空だから,それを充足する真理値割り当て M として
あらゆるものが許される.あらゆる真理値割り当てがψを充足するということは,
ψが恒真であるということに他ならない.
【注意】
x1
x2
・・・
xn
φ
4. 論理式の同値性・恒真性・充足関係
4.1 論理式の同値性
二つの異なる論理式が内容的にまったく同じことを
表わしていることがある.そのような論理式は
論理的に同値であるという.正確な定義は以下の
通りである.
φ ψ φ∨ψ ¬(φ∨ψ)
¬φ ¬ψ ¬φ∧¬ψ
T T T F
F F F
T F T F
F T F
F T T F
T F F
F F F T
T T T
4.2 論理式の恒真性・恒偽性
状況によらない絶対的な真理を表わす論理式が恒真式,
その否定が恒偽式である.正確な定義は次のようになる.
φ ψ φ→ψ
φ∧(φ→ψ) (φ∧(φ→ψ))→ψ
T T T
T T
T F F
F T
F T T
F T
F F T
F T
4.3 論理式の同値変形
論理式の同値性や恒真性を上のように定義に戻って
確かめることは,微積分で導函数や定積分の計算を
定義に戻って行うようなものである.命題変数の数が
増えたり論理式が複雑になるにつれて効率が悪くなる.
(a∧b)→(¬c∨¬d) ≡ ¬(a∧b)∨(¬c∨¬d)
≡ ¬a∨¬b∨¬c∨¬d
4.4 真理値割り当てと論理式の充足関係
恒真式は絶対的真実を表わしている.それに対して,
たとえば箱とボールのパズルの例は,ある条件の下で
何が成立するかを問題にしている.このような関係は
一般に充足関係として定式化される.
という二つの条件を表わす.このとき
M[a] = T, M[b] = T, M[c] = F という真理値割り当てはφを
充足する(すなわちパズルの解である)が,
M[a] = T, M[b] = T, M[b] = F という真理値割り当てはφを
充足しない.φ を充足する真理値割り当てはこれ以外にもいくつか
ある(捜してみよ).
4.5 意味論的演繹関係
恒真性 |=ψ はいわば絶対的な真理であるが,
ある前提のもとで成り立つこと(いわば相対的な真理)
を表わすのが次の「意味論的演繹関係」である.
キーワード
命題,命題変数,充足問題,ビット,論理回路,ブール函数,
真理値,真理値割り当て,論理演算子,真理表,命題定数,論理結合子,
論理式,原子式(原子命題),帰納的(再帰的)定義,
演算の優先順位,真理値割り当て,論理式の解釈,論理的同値性,恒真式,
恒偽式,部分論理式,同値変形,充足関係,モデル,充足可能性,
意味論的演繹関係