ルネサンスにおける代数学の発展
目次
- 1040-1123 オマル-ハイヤーム
- 1170-1240 フィボナッチ
- 14c-15c フローレンスの数学者
- 1445-1509 ルカ・パチオリ
- 1465-1526 スキピオネ・デル・フェルロ
- 1499-1557 ニコロ・タルタリア
- 1501-1576 ジェロラモ・カルダノ
- 1540-1603 フランソワ・ヴィエト
- 1548-1620 シモン・ステヴィン
- 1596-1650 ルネ・デカルト
- 1601-1665 ピエール・ド・フェルマ
- 参考文献
総目次へ戻る
(回)1040-1123 オマル-ハイヤーム
「ルバイヤート」の作者、哲学者、数学者、天文学者。
3 次方程式を考察。しかし「平方の平方」のような
「3 次元以上の量」は考えなかった。
11c スペインに回教の大学さかえる。製紙技術も伝わったらしいが後に回教勢
力が退くとともにすたれた。このころはまだヨーロッパには位取り記数法さえ
知られていなかった。
1096-1185 十字軍。
セルジュク朝がキリスト教徒の巡礼を認めなかったことによるという。
目次に戻る
1170-1240 フィボナッチ(ピサのレオナルド)
商人の父親と北アフリカを旅し、アル・フワリズミのアラビア数字と
位取り記数法を学ぶ。「実用幾何学」(96 角形を用いたπの計算が示される)、
および「算法の書」Liber Abaci (1202) などを書くが
広まる迄には二〜三百年を要した。
1241 ポーランドに蒙古軍
目次に戻る
14c-15cのフローレンスに
ベネディット、ビアギオ、アントニオ・マジンギィなどの数学者
このころイギリスで機械時計。1354ストラスブール、1450ボローニャでも時計
台。(なおギリシャ時代にも日時計、水時計があり、プラトンによりアテネに
も導入されていた。)
15c バスコ・ダ・ガマ、インドへ
1450 グーテンベルクの活版印刷術。完成と同時に債権者に返済を迫られて差
押えをうけ、本人の晩年は借金返済の重圧を負い不幸だったという。ただちに
ルターらの宗教改革、エラスムスらの人文主義(ユマニスト)を可能ならしめた
他、その影響ははかりしれない。
目次に戻る
1445-1509 ルカ・パチオリ
加法を p, 減法を m で、また未知数を co, その二乗、三乗を ce, cu 等と表わす
(ラテン語の正方形、立方体の頭文字)。
また 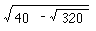 を RV40mR320 (V はカッコにあたる)と書く。
3次、4次の方程式については一般的解法が知られていないと述べた。1494「数
学大全」:代数・三角法・簿記・透視画法。レオナルド・ダ・ヴィンチとも親
交。1497「神聖比例論」(文字のデザインの方法、その他)、挿絵は全てダ・ヴィ
ンチによる。
を RV40mR320 (V はカッコにあたる)と書く。
3次、4次の方程式については一般的解法が知られていないと述べた。1494「数
学大全」:代数・三角法・簿記・透視画法。レオナルド・ダ・ヴィンチとも親
交。1497「神聖比例論」(文字のデザインの方法、その他)、挿絵は全てダ・ヴィ
ンチによる。
1499 ルイ12世軍ミラノに侵攻。
目次に戻る
1465-1526 スキピオネ・デル・フェルロ
3 次方程式の根号による解法(解の公式)。本は出さず、弟子のみに秘伝を伝えた。
目次に戻る
1499-1557 ニコロ・タルタリア
(「どもる人」、本名は Fontana)
ヴェニスの数学教師。スキピオネ・デル・フェルロの弟子アントニオ・マリア・
フィオレとシエナで「数学試合」。「試合」は当時の学者の地位を確立する場
であり、またお祭りでもあったという。それぞれパトロンがついて生活を支援した。
30問の問題を出しあって、期日までに沢山解いた方が勝ち。負けた方が解けなかっ
た問題の数だけ相手の友人を呼んで宴会を開かなくてはならなかったとも、あ
るいは解けなかった数だけの宴会を開かなくてはならなかったともいう。出さ
れた多くは3次方程式を解く問題であった。タルタリアはフェルロ達が解の公
式を持っていることを伝え聞き、それを期日の数日前に独自に発見して試合に
勝った。フェルロの方は師の教えを十分理解していなかったのか、出された問
題をほとんど解けずに終った。タルタリアは鷹揚なところを見せ、名誉のみで
満足し宴会を辞退したという。
目次に戻る
1501-1576 ジェロラモ・カルダノ
本業は医師、また占星術家。タルタリアの
発見を聞き、その方法を知りたいと願い、1539 にタルタリアと会う。(領主に
紹介することと引き換え。タルタリアにとっても彼の軍事技術を売りこむ好機
であった。)カルダノは神に誓って公開しないと言い、タルタリアは彼に自分
の方法を口伝した。カルダノはそれをすぐには理解しなかったが、努力して証
明を得た。そして、その方法がすでにスキピオネ・デル・フェルロが得ていた
ものであることを聞き、その遺稿を確認。かくてタルタリアとの誓いは意味を
失い、カルダノは1545に「アルス・マグナ」(偉大な方法)を著す。負の数、お
よびその平方根がほとんど初めて使用された。この中では彼自身の弟子ロドヴィ
コ・フェラリ(1522-1565)による4次方程式の解法も述べられた。
代数学のあるべき姿を示した点で画期的。ちなみにカルダノ自身は病弱で迷信
的な、かつ賭博好きな人間で、彼の人生の宗教的解釈を
後世にゆだねるべく、自伝「わが人生の書」を著し没す。
タルタリアは自分で発表するつもりだった内容を盗まれたと思ってカルダノの
本に激怒し、再三カルダノを告発。カルダノはしかし応ぜず、フェラリが公開
討論をすることになった。タルタリアは(「どもり」でもあり)これに消極的だっ
たというが、パトロンの名誉の手前応ぜざるを得なかった。フェラリは口達者だった
ので(粗暴だったともいう)勝敗は始めから明かで、この後失意のタルタリアは消
沈して健康を害し他界。しかし、タルタリアは何冊かの教科書を出版してその
影響は画家やイエズス会のカリキュラム、更にはガリレオにも及んだという。
彼らはまだ、例えば「x3+6x=20」が
「ひとつの立方体とその辺の6倍は20に等しい」と文章で
述べている。カルダノは複素数の解も見いだしたが、自分で
も懐疑的で「精神的苦しみ」を忘れて計算せよと述べた。
目次に戻る
1540-1603 フランソワ・ヴィエト
ポワチエ大学で法律を学び、貴族の家庭教師として
地理と天文を講義、出版。後に議会顧問、大審院判事。アンリIV世
(ブルボン朝、1610 旧教徒に暗殺される)に暗号解読などで仕え、
「数学試合」的な場で 45 次方程式を解いた(問題の方程式が sin
の 45倍角から生ずるものであることを見抜いた)。
方程式の未知数を母音字、係数を子音字でどちらも文字ひとつで表わし、
文章と数式の中間的な略記表現を用い、
例えば 3BA2 -DA +A3=Z は
B3 in A quad - D plato in A + A cubo aequatur Z solido と記した。
代数記法の祖とされる。負の解は認めなかった。
目次に戻る
1548-1620 シモン・ステヴィン
オランダ(1581に独立宣言)で活躍した技術者。
風車、鍵、港湾などを設計。十進数表示や筆算によるかけ算を普及させ、
+, −, √ なども用いた。×,÷は M, D と表示。負数、無
理数も避けることなく用いたが負数の平方根は認めなかった。アルキメデスを
理想とし、コペルニクス説(「天球回転論」1543)を擁護。容器の底における水
圧が容器の形によらず水位のみできまることを発見。
目次に戻る
1596-1650 ルネ・デカルト
哲学者、数学者:「我思う故に我あり」。「方法叙説」
の一部として解析幾何(座標の方法、ただし直交座標とは限らぬ)を発表。この
中ではじめて現在とほぼ同じ代数記号が用いられたが、原点も負の数もまだ使
われてはいない。また「長さ」と「面積」を比べるときにも、前者に単位の長
さを掛けてから行なっている。
目次に戻る
1601-1665 ピエール・ド・フェルマ
本職は法律家。「フェルマの最終定理」
(=ワイルズの定理 1995)を予想し、「証明を書くにはこの本の余白は狭すぎる」
と書き遺したが、彼の持っていた「証明」は何かの勘違いであったろうと思わ
れる。賭博の問題や、曲線に接線を引く問題も考察。
目次に戻る
参考文献
-
van der Wearden 「代数学の歴史」現代数学社
-
S.G.ギンディキン 「ガリレオの17世紀」「ガウスが切り開いた道」シュプリンガー東京
-
山下純一 「数学ものがたり」東京出版
-
アンドレ・ヴェイユ 「数論-歴史からのアプローチ」日本評論社
-
ブルバキ「数学史」東京図書
-
小堀憲 「数学史」 朝倉書店
-
カジョリ「初等数学史」(上下) 共立全書
-
長尾茂武 「建築家レオナルド・ダ・ヴィンチ」中公新書
-
佐々木力 「科学革命の歴史構造」(上下) 講談社学術文庫
目次へ戻る
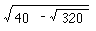 を RV40mR320 (V はカッコにあたる)と書く。
3次、4次の方程式については一般的解法が知られていないと述べた。1494「数
学大全」:代数・三角法・簿記・透視画法。レオナルド・ダ・ヴィンチとも親
交。1497「神聖比例論」(文字のデザインの方法、その他)、挿絵は全てダ・ヴィ
ンチによる。
を RV40mR320 (V はカッコにあたる)と書く。
3次、4次の方程式については一般的解法が知られていないと述べた。1494「数
学大全」:代数・三角法・簿記・透視画法。レオナルド・ダ・ヴィンチとも親
交。1497「神聖比例論」(文字のデザインの方法、その他)、挿絵は全てダ・ヴィ
ンチによる。