概要

一般にはDFT+Uを使ってバンドギャップの精度を増すことができるが、場合によってはそのまま計算しただけでは基底状態にならないこともある。ここでは例として反強磁性体FeOが単純にはうまく計算できないことと、その解決方法を示す。

このページは以下のスライドを参考に作成したので、詳しく知りたい場合はそちらを参照してください。

http://www.iiserpune.ac.in/~smr2626/hands_on/week1/july4/hands-on_dft_pu_last.pdf

なお、FeOのバンドギャップは光学吸収測定により2.4eVと見積もられている。

H. K. Bowen, D. Adler, and B. H. Auker, J. Solid State Chem. 12, 355 (1975).

DFT+U

まずは普通に計算してみよう。

FeO.scf.in

&control
   calculation='scf',
   prefix='FeO',
   pseudo_dir = './',
   outdir='./tmp/'
/
&system
   ibrav=0, 
   celldm(1)=8.19,
   nat=4, 
   ntyp= 3,
   ecutwfc = 30.0, ecutrho = 240.0,
   occupations='smearing', 
   smearing='mp', 
   degauss=0.02,
   nspin=2, 
   starting_magnetization(2)= 0.5, 
   starting_magnetization(3)=-0.5,
   lda_plus_u = .true.,
   Hubbard_U(2) = 4.0,
   Hubbard_U(3) = 4.0,
/
&electrons
/
CELL_PARAMETERS
 0.50 0.50 1.00
 0.50 1.00 0.50
 1.00 0.50 0.50
ATOMIC_SPECIES
 O    16.00  O.pbe-rrkjus.UPF
 Fe1  55.85  Fe.pbe-nd-rrkjus.UPF
 Fe2  55.85  Fe.pbe-nd-rrkjus.UPF
ATOMIC_POSITIONS crystal
 O   0.25 0.25 0.25
 O   0.75 0.75 0.75
 Fe1 0.0  0.0  0.0 
 Fe2 0.5  0.5  0.5
K_POINTS automatic
 4 4 4 1 1 1

FeO.nscf.in

&control
   calculation='nscf',
   prefix='FeO',
   pseudo_dir = './',
   outdir='./tmp/'
/
&system
   ibrav=0, 
   celldm(1)=8.19,
   nat=4, 
   ntyp= 3,
   ecutwfc = 30.0, ecutrho = 240.0,
   occupations = 'tetrahedra',
   nspin=2,
   starting_magnetization(2)= 0.5, 
   starting_magnetization(3)=-0.5,
   lda_plus_u = .true.,
   Hubbard_U(2) = 4.0,
   Hubbard_U(3) = 4.0,
/
&electrons
/
CELL_PARAMETERS
 0.50 0.50 1.00
 0.50 1.00 0.50
 1.00 0.50 0.50
ATOMIC_SPECIES
 O    16.00  O.pbe-rrkjus.UPF
 Fe1  55.85  Fe.pbe-nd-rrkjus.UPF
 Fe2  55.85  Fe.pbe-nd-rrkjus.UPF
ATOMIC_POSITIONS crystal
 O   0.25 0.25 0.25
 O   0.75 0.75 0.75
 Fe1 0.0  0.0  0.0 
 Fe2 0.5  0.5  0.5
K_POINTS automatic
 8 8 8 0 0 0

FeO.dos.in

&dos
   prefix='FeO',
   outdir='./tmp/',
   DeltaE=0.01
/

$ pw.x < FeO.scf.in > FeO.scf.out
$ pw.x < FeO.nscf.in > FeO.nscf.out
$ dos.x < FeO.dos.in > FeO.dos.out

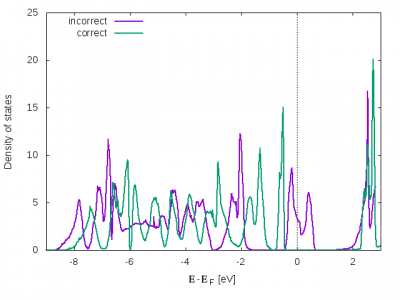
状態密度を描いてみればわかるように金属となってしまう。実は、基底状態ではない準安定なところに収束してしまったため、このような結果になってしまう。

問題の検討

FeO.scf.outで一回目のSCF計算が終わった部分を見てみると、次のようになっている。

FeO.scf.out

（略）
     iteration #  1     ecut=    30.00 Ry     beta=0.70
     Davidson diagonalization with overlap
     ethr =  1.00E-02,  avg # of iterations =  2.2
 --- enter write_ns ---
 LDA+U parameters:
U( 2)     =  4.00000000
alpha( 2) =  0.00000000
U( 3)     =  4.00000000
alpha( 3) =  0.00000000
atom    3   Tr[ns(na)] (up, down, total) =   4.99738  1.04703  6.04441
   spin  1
    eigenvalues: 
  0.999  0.999  0.999  1.000  1.000
    eigenvectors:
  0.000  0.018  0.016  0.527  0.438
  0.333  0.589  0.054  0.021  0.002
  0.333  0.033  0.610  0.001  0.022
  0.000  0.016  0.018  0.438  0.527
  0.333  0.343  0.301  0.013  0.010
    occupations:
  1.000 -0.000 -0.000 -0.000 -0.000
 -0.000  0.999 -0.000 -0.000  0.000
 -0.000 -0.000  0.999  0.000  0.000
 -0.000 -0.000  0.000  1.000 -0.000
 -0.000  0.000  0.000 -0.000  0.999
   spin  2
    eigenvalues: 
  0.166  0.166  0.204  0.256  0.256
    eigenvectors:
  0.513  0.459  0.000  0.001  0.026
  0.017  0.001  0.333  0.576  0.073
  0.001  0.017  0.333  0.376  0.273
  0.459  0.513  0.000  0.026  0.001
  0.010  0.009  0.333  0.021  0.627
    occupations:
  0.169 -0.006 -0.006 -0.000 -0.012
 -0.006  0.237 -0.016 -0.010  0.016
 -0.006 -0.016  0.237  0.010  0.016
 -0.000 -0.010  0.010  0.169 -0.000
 -0.012  0.016  0.016 -0.000  0.237
atomic mag. moment =     3.950343
（略）

ここで注目したいのが、atom 3（Feのアップスピンサイト）のspin 2（ダウンスピン）のeigenvaluesである。

 spin  2
  eigenvalues: 
0.166  0.166  0.204  0.256  0.256

固有値(eigenvalue)が大きいほどエネルギー準位が低い。もともとの格子は立方対称なので準位の低い三重縮退のt2g軌道と、高い二重縮退のeg軌道に分裂している。反強磁性秩序によってt2g軌道の対称性が壊れて二重縮退の準位(0.256)と縮退のない準位(0.204)に分裂している。

Feは価電子を6つ持っているので、フントの規則によりegとt2gのすべてにアップスピンの電子がすべて詰まったのち、残りの1つがダウンスピンとしてどこかの準位に入る。すなわち、もしも系が絶縁体なのであれば、このダウンスピンの準位は縮退のない準位に入らなければならない（縮退のあるバンドに電子が1つだけ入れば、バンドが中途半端に満たされるので金属となる）ので、縮退のない準位はもっとも大きい固有値にならなければならない。しかし、FeO.scf.outの結果を見てわかるように、縮退のない準位は固有値がもっとも小さくなってしまっている。

FeO.scf.out

（略）
     End of self-consistent calculation
 --- enter write_ns ---
 LDA+U parameters:
U( 2)     =  4.00000000
alpha( 2) =  0.00000000
U( 3)     =  4.00000000
alpha( 3) =  0.00000000
atom    3   Tr[ns(na)] (up, down, total) =   4.98974  1.73816  6.72790
   spin  1
    eigenvalues: 
  0.996  0.996  0.999  1.000  1.000
    eigenvectors:
  0.680  0.304  0.000  0.004  0.012
  0.009  0.002  0.333  0.656  0.000
  0.000  0.011  0.333  0.164  0.492
  0.304  0.680  0.000  0.012  0.004
  0.007  0.003  0.333  0.164  0.492
    occupations:
  0.996 -0.000 -0.000 -0.000 -0.000
 -0.000  0.999 -0.000 -0.000  0.000
 -0.000 -0.000  0.999  0.000  0.000
 -0.000 -0.000  0.000  0.996 -0.000
 -0.000  0.000  0.000 -0.000  0.999
   spin  2
    eigenvalues: 
  0.099  0.221  0.221  0.599  0.599
    eigenvectors:
  0.000  0.544  0.342  0.008  0.105
  0.333  0.066  0.010  0.555  0.036
  0.333  0.002  0.074  0.287  0.303
  0.000  0.342  0.544  0.105  0.008
  0.333  0.047  0.029  0.044  0.547
    occupations:
  0.264 -0.049 -0.049 -0.000 -0.098
 -0.049  0.403 -0.152 -0.085  0.152
 -0.049 -0.152  0.403  0.085  0.152
 -0.000 -0.085  0.085  0.264 -0.000
 -0.098  0.152  0.152 -0.000  0.403
atomic mag. moment =     3.251583
（略）

このように、本来ほしい状態と違う状態に収束してしまうのを避けるため、starting_ns_eigenvalueというものを使う。

starting_ns_eigenvalue

FeO.scf.inをコピーし、$systemにstarting_ns_eigenvalueを追加した以下の入力ファイルを作成する。

FeO_2.scf.in

&control
   calculation='scf',
   prefix='FeO',
   pseudo_dir = './',
   outdir='./tmp/'
/
&system
   ibrav=0, 
   celldm(1)=8.19,
   nat=4, 
   ntyp= 3,
   ecutwfc = 30.0, ecutrho = 240.0,
   occupations='smearing', 
   smearing='mp', 
   degauss=0.02,
   nspin=2, 
   starting_magnetization(2)= 0.5, 
   starting_magnetization(3)=-0.5,
   lda_plus_u = .true.,
   Hubbard_U(2) = 4.0,
   Hubbard_U(3) = 4.0,
   starting_ns_eigenvalue(3,2,2)=1.0, 
   starting_ns_eigenvalue(3,1,3)=1.0,
/
&electrons
/
CELL_PARAMETERS
 0.50 0.50 1.00
 0.50 1.00 0.50
 1.00 0.50 0.50
ATOMIC_SPECIES
 O    16.00  O.pbe-rrkjus.UPF
 Fe1  55.85  Fe.pbe-nd-rrkjus.UPF
 Fe2  55.85  Fe.pbe-nd-rrkjus.UPF
ATOMIC_POSITIONS crystal
 O   0.25 0.25 0.25
 O   0.75 0.75 0.75
 Fe1 0.0  0.0  0.0 
 Fe2 0.5  0.5  0.5
K_POINTS automatic
 4 4 4 1 1 1

ここで、starting_ns_eigenvalueの意味は次のとおりである。

変数	説明
starting_ns_eigenvalue(m,i,n)	n番目の原子のi番目のスピンの、m番目の固有値にある電子数の初期値

ここでm=3としているのは、FeO.scf.outで1回目のSCF計算で縮退していない固有値が左から3番目だったからである。縮退のない準位に電子が入ってほしかったことを思い出そう。

$ pw.x < FeO_2.scf.in > FeO_2.scf.out

さきほどの全エネルギーと比較すると、今回のほうが安定になっていることがわかる。

FeO.scf.out

!    total energy              =    -175.09491797 Ry

FeO_2.scf.out

!    total energy              =    -175.17890387 Ry

状態密度の計算はさきほどと同様に行う。ギャップが開いていることがわかる。

Table of Contents

概要

DFT+U

問題の検討

starting_ns_eigenvalue