我々は、破壊現象を非平衡統計物理学の立場から研究しています。図は、我々のモデルにおいて、完全にこわれる寸前で系に存在する亀裂の様子を示しています。藍色の点が亀裂を表しており、他の点の色は、そこにかかる応力の強さを表しています。我々は、例えばこのようなシミュレーションにより、破壊現象における普遍性を明かにしようとしています。我々は、破壊現象を非平衡統計物理学の立場から研究しています。図は、我々のモデルにおいて、完全にこわれる寸前で系に存在する亀裂の様子を示しています。藍色の点が亀裂を表しており、他の点の色は、そこにかかる応力の強さを表しています。我々は、例えばこのようなシミュレーションにより、破壊現象における普遍性を明かにしようとしています。
物体の破壊は、自然界にしろ工学的な構造物にしろ、私達の身の回りで日常的に見られる非平衡現象の一つです。破壊現象の理解は、例えば、破壊しづらい材料の設計や材料の効率的な破壊の手法、破壊の制御や予測などの技術につながり、巨大な建築物からナノスケールのデバイスに至るまで、様々な応用が期待できます。そのため、破壊現象は大昔から科学と工学の基礎的な研究問題でありつづけています。
破壊研究の歴史は長く、ヨーロッパにおける現代科学の黎明期であったルネサンス期、Leonardo da Vinciによる金属ワイヤーの強度のサイズ依存性に関する研究[1]にまで遡ることができるそうです[2]。また、19世紀の終わり、すなわち産業革命以降、橋や建物、船舶などといった、工学的構造物の巨大化が進み、そのような構造物の破壊による災害が深刻化してきました。このような歴史的背景のもと、特に20世紀、破壊力学と呼ばれる、亀裂を内包するような物体がどれだけ応力に対して耐えられるかを記述する研究分野が発達しました。破壊力学はAlan Arnold GriffithやGeorge Rankine Irwinらの有名な研究をその起源としています。他にも、多数のクラックを有する物体の破壊特性の理論としては、極値統計(extreme value statistics) [3]に基づく手法や、損傷力学と呼ばれる、弾性体に損傷場を導入したものなどがあります。
今後も、ナノテクノロジーの発展に伴い、破壊現象の理解はより重要になっていくでしょう。ナノスケール、マイクロスケールの物体では、破壊力学のようなこれまでの連続体力学による手法が適用できるかどうかは決して自明ではありません。なぜなら、系が小さいが故に、熱揺らぎや量子効果が無視できなくなる可能性があるからです。
ここ20年ほど、統計物理学の立場から破壊現象にアプローチした研究が増えてきています[2]。これにはいくつか理由があります。
物体は普通、多くの欠陥や揺らぎを持っています。そのため、破壊現象というのは本来、従来の統計物理においてなされてきたように、統計的、確率的手法を用いて取り扱わなければならないものです。しかしながら、破壊に関する古典的な研究では、この問題にはあまり注意が払われてきませんでした。この理由の一つとしては、破壊力学などで利用されている連続体力学に乱れを導入するのは、出来なくはないが大変難しい、ということが挙げられます。
より基礎的な視点では、破壊過程とは、長距離相互作用をする乱雑系における非可逆的な動力学であるとみなせます。したがって、破壊現象は、平衡から遠く離れた系のよい研究対象であると言えます。この30年ほど、様々な系の非平衡状態について盛んに研究がなされています。例えば、平衡状態や平衡に近い線形非平衡状態における統計力学の手法や考え方を破壊現象などの非平衡状態に拡張できるのか、というのは興味深い問題です。
計算機の発達も重要な理由の一つです。破壊現象は非常に複雑で、特に強い乱れがある状況では、例え単純な模型に問題を落としても、計算機を全く用いずに意義のあることを主張するのは一筋縄ではいきません。近年の計算機の能力は昔と比べ非常に大きくなり、ランダムヒューズ模型[2]やランダムバネ模型[4]、あるいは、我々も取り扱ったファイバーバンドル模型[5]のような、余程近似をしない限り手で解くのは非常に困難だが、破壊現象の本質を十分に保ったまま単純化を行ったような模型について、多くの研究がなされるようになりました。さらに最近では、分子動力学法など、より第一原理的な手法による破壊の研究もなされるようになり[6, 7]、今後も計算資源の増大による破壊現象の研究の発展が期待できます。
ここでは、我々が最近行っている破壊現象に関する研究を紹介します。我々は、数ある破壊形態の中でも特に、熱活性破壊と呼ばれる、熱により活性化された微小亀裂が引き起こすクリープ破壊について研究をしています[8]。
普通、破壊は、物体にかけた応力がある臨界値を越えると生じます。しかしながら、実際には、物体にかけた応力がその臨界応力より低くても、しばらくかけつづけることでも破壊は生じえます。このような破壊現象はクリープ破壊や亜臨界破壊と呼ばれ、様々な物理系、生物系、地球科学系などで見られる非常に重要な破壊形態であることが知られています[9, 10]。
なぜクリープ破壊が起こるのか、そのメカニズムとしては幾つか可能性が考えられます。例えば、物体の構成要素が粘弾性応答をする場合、その構成要素に荷重がかかってから実際に亀裂が生じるまでの間にタイムラグが生じえます。他にも、構成要素間に摩擦力が働く場合、物体のある箇所に亀裂が生じてから周囲に応力集中が伝わるのに時間がかかる、ということが考えられます。
最近、熱により活性化された微視的な亀裂の生成がクリープ破壊の原因となりうる、という驚くべき発見がいくつか報告されるようになりました。例えば、熱活性による遅い亀裂の進行により、破断面の乱雑さが影響されうる、という研究があります[11]。熱活性による損傷の集積の結果生じる巨視的な破断は、しばしば予想も出来ない急なイベントとして起こります。このような破壊の予測のためには、臨界点に近づくときの測定量間の関係を知ることが非常に重要となります。
我々は、ファイバーバンドル模型[5]と呼ばれる枠組みを用いて、熱活性破壊において亀裂の周囲における応力集中の影響を調べました。
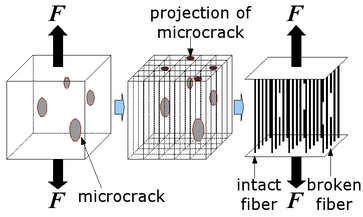ファイバーバンドル模型とは、破壊現象を取り扱うためのミニマルモデルです。今、2枚の板の間に、たくさんの繊維(ファイバー)が並行に繋がっているとします。各ファイバーにはそれぞれ、与えられた荷重に対する臨界強度が決まっており、糸にかかる荷重がその強度を越えるとその糸は切れてしまいます。このファイバーの束(ファイバーバンドル)をファイバーと同じ向きに引っ張ることを考えます。すると、ある応力のもとで、幾つかのファイバーにかかる荷重はその臨界強度を超え、切れてしまいます。このとき、系のエネルギーが保存すると仮定すると、その壊れたファイバーにかかっていた荷重は近くのファイバーに移動することになります。このような荷重の移動により、新たに壊れてしまうファイバーが出てきます。この繰り返しにより、破壊の雪崩(バースト)が発生します。
我々は、熱活性破壊を調べるため、このファイバーバンドル模型に熱揺らぎの効果を導入しました。具体的には、各ファイバーの強度が時間とともに揺らぐとしています。この状況のもとで、寿命のサイズ依存性やバーストの統計分布について非自明な結果を得ました[8]。この結果は、材料設計や破壊予測に繋がる可能性のある、興味深いものです。