ガラス転移に対する場の理論的アプローチ
ガラスは、古代メソポタミアやエジプトで造られて、今も窓ガラスに限らず重要な物質形態であるが、統計熱力学的性質はよく分かっておらず、
未だに研究のフロンティアである。またガラスに関連した状態はスピングラス、超伝導ガラスやハドロンのカラーグラス等で普遍的に観測されてい
る。現在では、少なくとも古典的なガラス相は熱力学的な相ではなく粘性率が異常に大きい過冷却液体の準安定な状態を指すものと理解されている。
そのため、動的にガラス転移を理解する必要があるが、それには誰も成功していない。ここで記憶力の良い読者は高密度系の粘性率の発散の仕方が
理解できていないというアインシュタイン以来の古典的課題を思い出すだろう。粘性率がどのように大きくなるのかが分からないが故にガラス転移
の物理が理解されていないと言い換えても良い。またガラス状物質にせん断等の外力をかけた非平衡定常状態の統計的性質は未だ解明されていない
が、続々と揺動散逸定理の破れや非線形応答理論の必要性が報告されている。即ち外力下での粘性率と外力がない場合の粘性率の意味が若干違うこ
とがまさに問題になっているのである。また液体状態と固体的な硬さや降伏応力を持つ相への相転移であるジャミング転移の問題も注目されている。
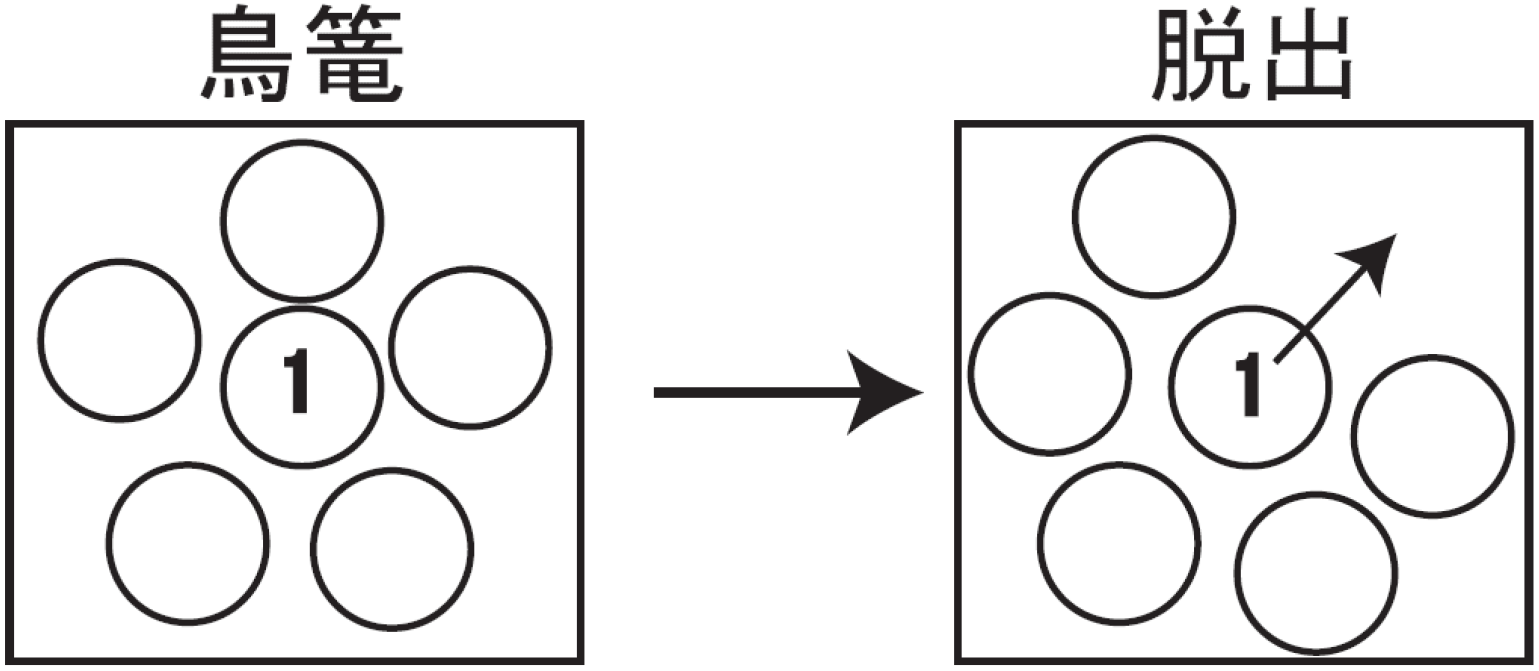図：ガラスのケージ状態とその脱出のメカニズム（当研究室出身西野貴博学位論文より）
ガラス転移についての特徴付けは密度の時間相関関数の時間発展によって行われる。この密度の時間相関は異なった時間で密度を測ってその積の
二体関数によって初期の情報がどのように失われていくかどうかの指標になっている。完全に凍結すればその密度相関関数は有限値を持ち続けるこ
とになる。実験等によると高温の液体状態では時間の指数関数に従いゼロまで減衰するが、ガラス転移点より低温になると途中で一定の値を持つ二
段階緩和が観測されるようになる。この密度相関関数が一定の値を持つ領域では、粒子が自ら作ったケージの中にトラップされて構造がほぼ凍結さ
れた準安定状態となっている。逆に言えばガラス状態は完全に構造が凍結した状態ではない。この二段階緩和は、未だにミクロなモデルから出発し
た統計物理的な理論解析で説明することに成功していない。最もスタンダードな統計物理学的理論では液体状態を仮定し、リュウビル(Liouville)方程
式と呼ばれる位相空間の分布関数から出発し、密度相関関数の従う四体相関を含む発展方程式を形式的に導き、その四体相関を二体相関の積に書き
換えることで得られた方程式を用いている。この理論はモード結合理論と呼ばれ、1970 年前後に臨界現象に伴う系の遅い変数のダイナミックスを記
述するときに大きな成功を収めた理論と基本的に同じである。しかし相関長が発散し、長距離構造の遅いダイナミックスで閉じ、ミクロの詳細に依
存しない臨界現象に比べて、ガラス転移では相関長の増大が自明には見えず、粒子スケールの構造が重要で、かつ単分散の液体では観測できない等
ミクロ構造の詳細に依存する現象であるからである。モード結合理論は、単分散の単純液体の理論であるが故に低温での完全な凍結を予言してしま
い、二段階緩和の予言に成功していない。またモード結合理論の考え方に従って粘性率を密度の時間相関関数の積分形で表すことが可能である。そ
の式を用いると完全な凍結は粘性率の発散を意味し、二段階緩和は大きな粘性率ではあるが発散をないことを意味している。実験は言うまでもなく
後者をサポートしている。
当研究室ではその問題に正面から取り組み、現象論的な非線形ランジュバン方程式から出発し、それに対して応答関数と相関関数双方を扱える場
の理論を構築し、ガラス転移をどう理解するかを探っている。
