ジャミング転移について
高密度粉体の物理とガラス転移の物理とは共通する側面が多い。
平衡状態近傍でのガラス転移は密度を固定して温度を変えたときに低温側でガラス状態になるとされてきた。
しかし温度ゼロの極限でせん断等の外力をコントロールした場合、
或いは密度を変えた場合には液体状の状態から動きの止まったガラス状の相に変化する。
この転移をジャミング転移と呼ぶ。
ジャミング転移は液体状態では物質の硬さがないものが硬さを持つ固体的な状態へ変化する相転移とも言えるし、
或いはせん断率がゼロの極限で降伏応力のない状態（接線応力がゼロ）から有限の降伏応力を持つ状態への相転移と捉えることも可能である。
我々のグループではこのジャミング転移の性質を調べるために、
個々の粉体粒子の接触モデルとして接線方向に働く摩擦力を無視したつるつるの粒子に対して現象論を導入し、
そのジャミング転移が連続転移であり、その連続転移を特徴付ける臨界指数を予言し、
その予言が正しいことを数値的に検証した。
またその副産物として粉体集団の粘性率がジャミング転移点近傍で臨界密度からのずれの４乗に反比例して発散することを発見した。
更に粒子接触のモデルを固定したらこれらの臨界指数は空間次元に依存しないことも見出した。
これは新しいタイプの非平衡相転移の性質を明らかにしたという意味で興味深い結果であると思われる。
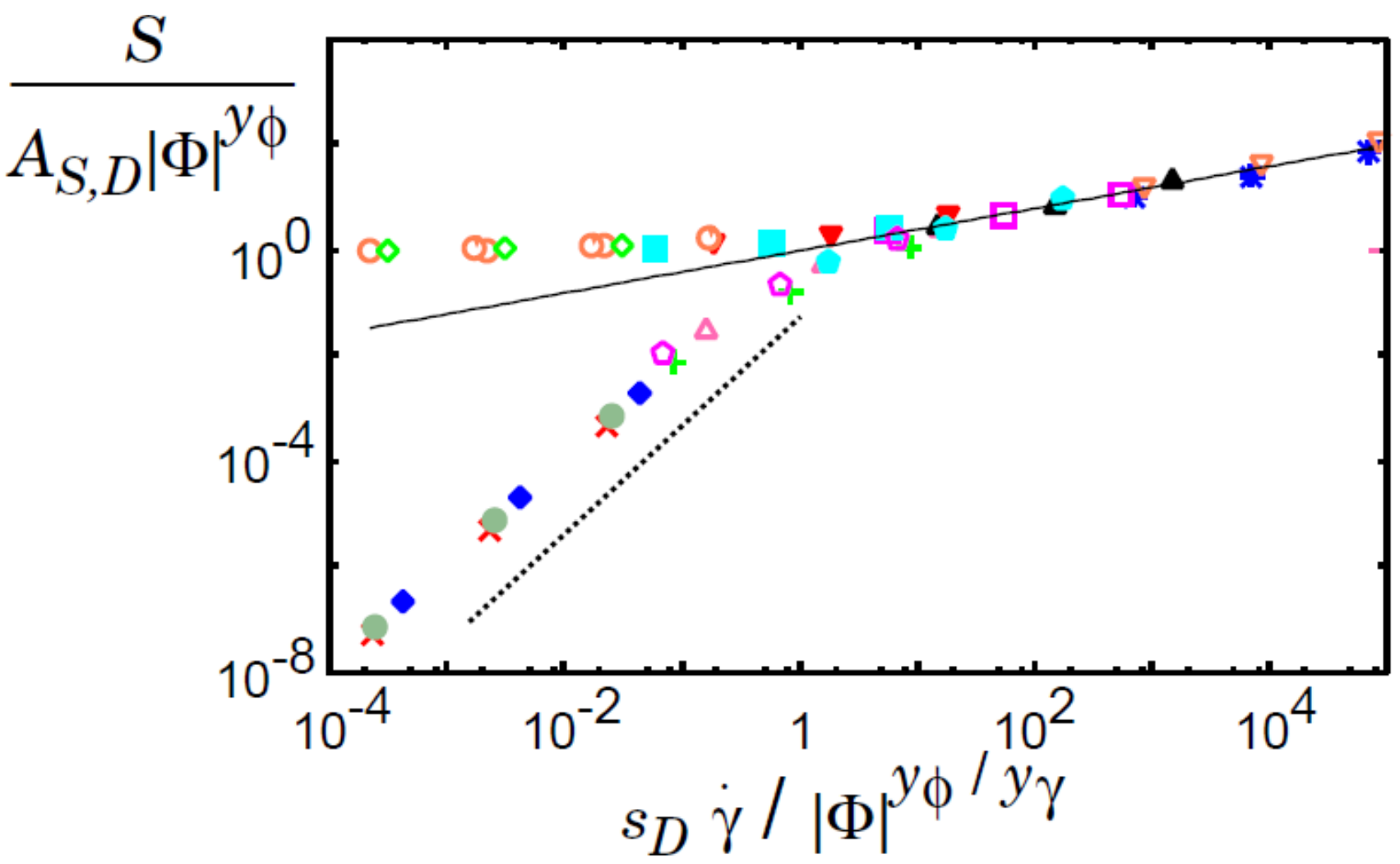図：接線応力Sのスケーリング。Φはジャミング密度からのずれ。yφ, yγはスケーリング指数。
様々な次元、Φのデータを重ね書きしたもの。
図の左側で水平に伸びている分枝はせん断速度がゼロの極限でも有限の降伏応力を持つことを示すジャミングを表し、
左下に伸びている分枝はせん断速度がゼロになると接線応力がゼロになる液体的分枝を表す。
(M. Otsuki and H. Hayakawa,Prog. Theor. Phys. 121, 647 (2009)より)
