
非平衡環境下での液体論
気体や固体に比べて液体に関する理解はまだまだ不満足な状態にある。例えば、流体の
基礎方程式である Navier-Stokes 方程式は気体に対して成り立つことの理論的証拠がある
が、液体に対して本当に満足のいく導出がないというと驚くだろうか。ましてせん断等の
外力が加わった非平衡環境下での液体論はまだ分かっていないことが多い。
 当研究室では非平衡液体論を発展させている。この研究の目的の一つはガラス転移にも
使われるモード結合理論の一般化を発展させることにあり、また別の目的は粉体のような
特異な液体と通常の分子液体の違いを明確にするためのものである。ひいてはジャミング
とガラス転移の共通点と相違点を明らかにしたい。最近、当研究室で得られた成果の一つ
はせん断系での長距離相関の理論的予測と粉体でも分子液体でも成り立つその普遍性であ
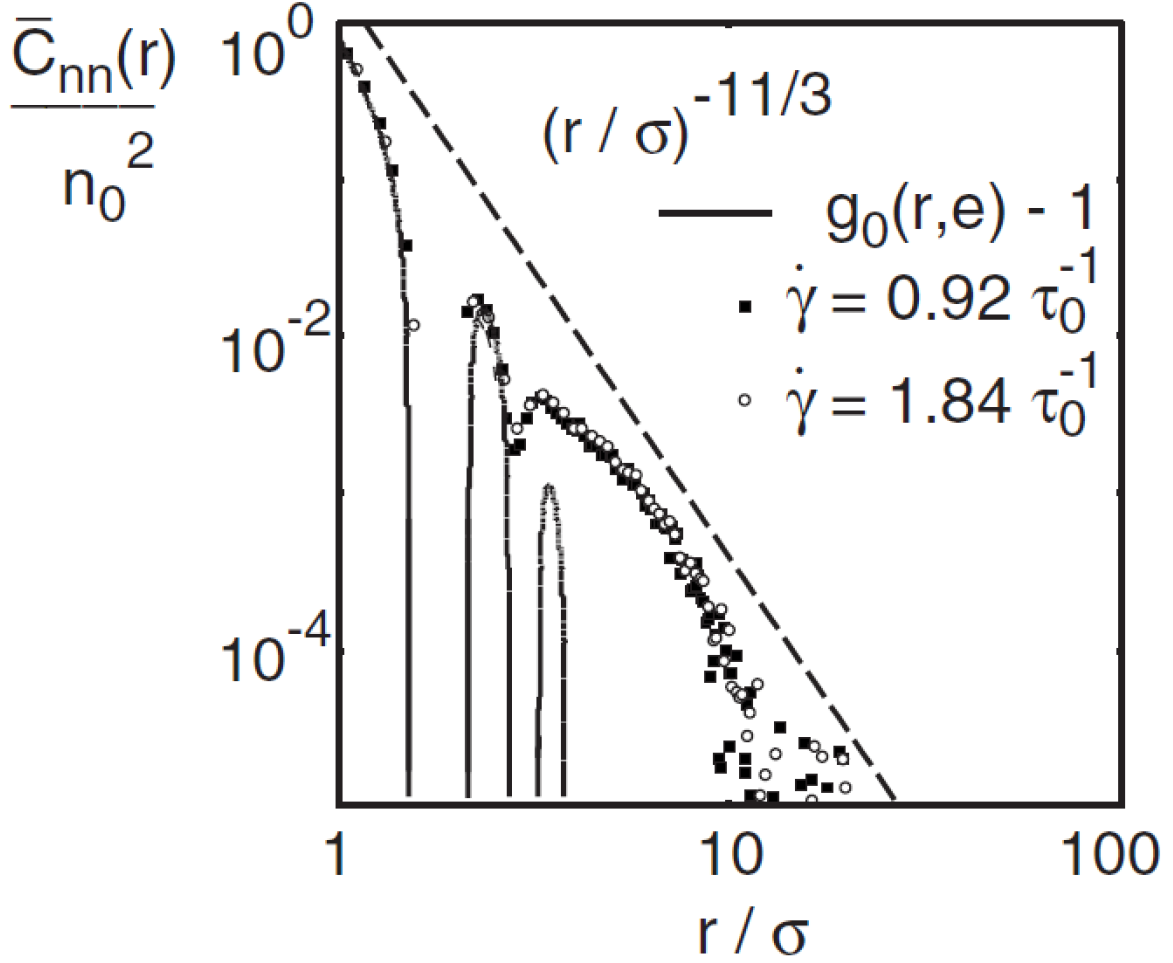
る。例えば下の図はせん断系での密度相関であるが、実線はせん断をかけないときに理論
的に予測された相関関数であり、破線はせん断をかけたときに現れる長距離相関である。(M.
Otsuki and H. Hayakawa, PRE 79, 021502 (2009)より)。このような長距離相関は速度相
関により強く現れるように非平衡環境下での液体に普遍的に現れる。
また輸送問題で最も基本的な量である粘性率に関しても、当研究室の研究から非常に面
白いことが分かってきた。古くはアインシュタインによって稀薄サスペンションの粘性率
が体積分率に比例する補正があることが指摘されていたが、それ以上の密度では一般論が
成り立たないという悲観的な見方が多数派であった。しかし当研究室の最近の研究による
と粘性率の発散する臨界密度近傍では新たな普遍的な法則が存在しそうであることが分か
りつつある。これらはジャミング転移の物理とも関連しており、今後の発展が待たれる分
当研究室では非平衡液体論を発展させている。この研究の目的の一つはガラス転移にも
使われるモード結合理論の一般化を発展させることにあり、また別の目的は粉体のような
特異な液体と通常の分子液体の違いを明確にするためのものである。ひいてはジャミング
とガラス転移の共通点と相違点を明らかにしたい。最近、当研究室で得られた成果の一つ
はせん断系での長距離相関の理論的予測と粉体でも分子液体でも成り立つその普遍性であ
る。例えば下の図はせん断系での密度相関であるが、実線はせん断をかけないときに理論
的に予測された相関関数であり、破線はせん断をかけたときに現れる長距離相関である。(M.
Otsuki and H. Hayakawa, PRE 79, 021502 (2009)より)。このような長距離相関は速度相
関により強く現れるように非平衡環境下での液体に普遍的に現れる。
また輸送問題で最も基本的な量である粘性率に関しても、当研究室の研究から非常に面
白いことが分かってきた。古くはアインシュタインによって稀薄サスペンションの粘性率
が体積分率に比例する補正があることが指摘されていたが、それ以上の密度では一般論が
成り立たないという悲観的な見方が多数派であった。しかし当研究室の最近の研究による
と粘性率の発散する臨界密度近傍では新たな普遍的な法則が存在しそうであることが分か
りつつある。これらはジャミング転移の物理とも関連しており、今後の発展が待たれる分



 当研究室では非平衡液体論を発展させている。この研究の目的の一つはガラス転移にも
使われるモード結合理論の一般化を発展させることにあり、また別の目的は粉体のような
特異な液体と通常の分子液体の違いを明確にするためのものである。ひいてはジャミング
とガラス転移の共通点と相違点を明らかにしたい。最近、当研究室で得られた成果の一つ
はせん断系での長距離相関の理論的予測と粉体でも分子液体でも成り立つその普遍性であ
る。例えば下の図はせん断系での密度相関であるが、実線はせん断をかけないときに理論
的に予測された相関関数であり、破線はせん断をかけたときに現れる長距離相関である。(M.
Otsuki and H. Hayakawa, PRE 79, 021502 (2009)より)。このような長距離相関は速度相
関により強く現れるように非平衡環境下での液体に普遍的に現れる。
また輸送問題で最も基本的な量である粘性率に関しても、当研究室の研究から非常に面
白いことが分かってきた。古くはアインシュタインによって稀薄サスペンションの粘性率
が体積分率に比例する補正があることが指摘されていたが、それ以上の密度では一般論が
成り立たないという悲観的な見方が多数派であった。しかし当研究室の最近の研究による
と粘性率の発散する臨界密度近傍では新たな普遍的な法則が存在しそうであることが分か
りつつある。これらはジャミング転移の物理とも関連しており、今後の発展が待たれる分
当研究室では非平衡液体論を発展させている。この研究の目的の一つはガラス転移にも
使われるモード結合理論の一般化を発展させることにあり、また別の目的は粉体のような
特異な液体と通常の分子液体の違いを明確にするためのものである。ひいてはジャミング
とガラス転移の共通点と相違点を明らかにしたい。最近、当研究室で得られた成果の一つ
はせん断系での長距離相関の理論的予測と粉体でも分子液体でも成り立つその普遍性であ
る。例えば下の図はせん断系での密度相関であるが、実線はせん断をかけないときに理論
的に予測された相関関数であり、破線はせん断をかけたときに現れる長距離相関である。(M.
Otsuki and H. Hayakawa, PRE 79, 021502 (2009)より)。このような長距離相関は速度相
関により強く現れるように非平衡環境下での液体に普遍的に現れる。
また輸送問題で最も基本的な量である粘性率に関しても、当研究室の研究から非常に面
白いことが分かってきた。古くはアインシュタインによって稀薄サスペンションの粘性率
が体積分率に比例する補正があることが指摘されていたが、それ以上の密度では一般論が
成り立たないという悲観的な見方が多数派であった。しかし当研究室の最近の研究による
と粘性率の発散する臨界密度近傍では新たな普遍的な法則が存在しそうであることが分か
りつつある。これらはジャミング転移の物理とも関連しており、今後の発展が待たれる分