
量子推定理論によるHeisenbergの不確定性関係の定式化
1927 年に Heisenberg はガンマ線顕微鏡による粒子の位置の測定の思考実験を考察することにより、位置
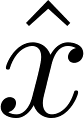 の測定誤差
の測定誤差
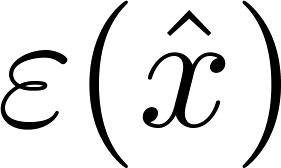 と測定による運動量
と測定による運動量
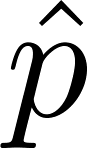 への擾乱
への擾乱
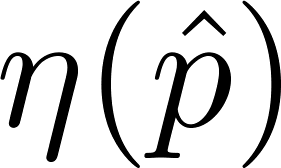 の間にトレードオフ関係
の間にトレードオフ関係
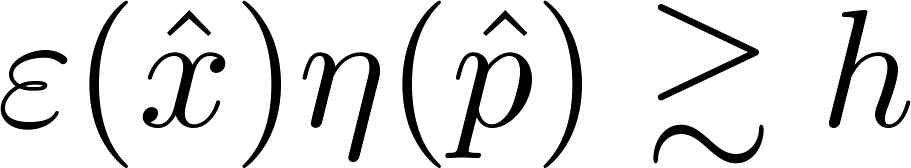 を見出した。このトレードオフ関係によって、ある物理量の測定をそれと共役な物理量への擾乱無しに行うことはできない、
という量子測定の相補性 (complementarity) が示唆された。
しかし、当時、量子測定についての理論はまだ完成していなかったため、
ガンマ線顕微鏡に限らない一般の測定過程における誤差と擾乱の間のトレードオフ関係が明らかにすることはできなかった。
さらに、同時期に発見された Kennard およびRobertson らによる量子揺らぎについてのトレードオフ関係
を見出した。このトレードオフ関係によって、ある物理量の測定をそれと共役な物理量への擾乱無しに行うことはできない、
という量子測定の相補性 (complementarity) が示唆された。
しかし、当時、量子測定についての理論はまだ完成していなかったため、
ガンマ線顕微鏡に限らない一般の測定過程における誤差と擾乱の間のトレードオフ関係が明らかにすることはできなかった。
さらに、同時期に発見された Kennard およびRobertson らによる量子揺らぎについてのトレードオフ関係
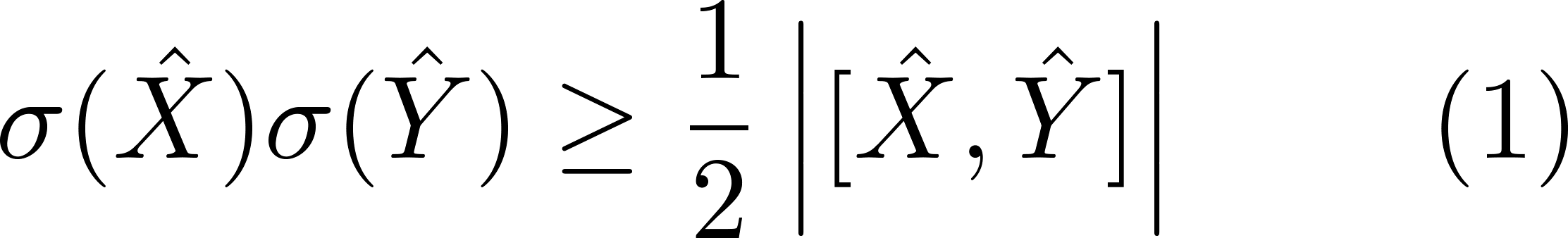 が Heisenberg の不確定性関係の数学的定式化であると誤って認識された。
しかしながら、量子揺らぎそのものは測定過程に依存せず、系に内在的な量であり、
したがって Robertson-Kennard の不等式は量子測定の誤差についてのトレードオフ関係ではない。
Robertson-Kennard の不等式に代表される、測定過程に依存しない、
対象となる量子系そのものの性質のみで表される不確定性関係は量子状態の非決定性 (indeterminacy) と呼ばれる。
近年の量子制御技術の発展によって、量子系に対する精密な測定が実現できるようになってきており、
量子測定の精度の限界を与える Heisenberg の不確定性関係が再び着目されるようになってきている。
これまで、量子測定の誤差は測定値の分散によって議論されてきた。しかし、測定値の分散が小さくても、
測定によって得られた情報量が多いとは一般に言えず、測定値の分散それ自身は測定の精度を表す指標にはな
らない。量子測定の相補性は、測定値の分散についてのトレードオフ関係ではなく、測定によって得られる互
いに非可換な物理量についての情報量の間にトレードオフ関係が存在することを示している。1970 年頃、量
子測定理論が Kraus や Davies らによって構築される一方、Helstrom や Holevo らによって量子推定理論の
基礎が研究された。量子推定理論は、例えば、未知の量子状態が与えられた場合、どのような測定を行えば量
子状態を効率よく推定できるかを明らかにする。推定精度が高いほど量子測定によって得られる情報量は多
く、逆に推定精度が低い場合には測定によって得られる情報量は少ない。したがって、現代的な観点からは、
Heisenberg の不確定性関係は測定によって得られたある物理量についての情報量と、測定過程による反作用
が引き起こす共役な物理量についての情報の損失の間のトレードオフ関係として捉えられる。
我々は、測定結果からの量子状態の推定精度を表す Fisher 情報量を用いて誤差
が Heisenberg の不確定性関係の数学的定式化であると誤って認識された。
しかしながら、量子揺らぎそのものは測定過程に依存せず、系に内在的な量であり、
したがって Robertson-Kennard の不等式は量子測定の誤差についてのトレードオフ関係ではない。
Robertson-Kennard の不等式に代表される、測定過程に依存しない、
対象となる量子系そのものの性質のみで表される不確定性関係は量子状態の非決定性 (indeterminacy) と呼ばれる。
近年の量子制御技術の発展によって、量子系に対する精密な測定が実現できるようになってきており、
量子測定の精度の限界を与える Heisenberg の不確定性関係が再び着目されるようになってきている。
これまで、量子測定の誤差は測定値の分散によって議論されてきた。しかし、測定値の分散が小さくても、
測定によって得られた情報量が多いとは一般に言えず、測定値の分散それ自身は測定の精度を表す指標にはな
らない。量子測定の相補性は、測定値の分散についてのトレードオフ関係ではなく、測定によって得られる互
いに非可換な物理量についての情報量の間にトレードオフ関係が存在することを示している。1970 年頃、量
子測定理論が Kraus や Davies らによって構築される一方、Helstrom や Holevo らによって量子推定理論の
基礎が研究された。量子推定理論は、例えば、未知の量子状態が与えられた場合、どのような測定を行えば量
子状態を効率よく推定できるかを明らかにする。推定精度が高いほど量子測定によって得られる情報量は多
く、逆に推定精度が低い場合には測定によって得られる情報量は少ない。したがって、現代的な観点からは、
Heisenberg の不確定性関係は測定によって得られたある物理量についての情報量と、測定過程による反作用
が引き起こす共役な物理量についての情報の損失の間のトレードオフ関係として捉えられる。
我々は、測定結果からの量子状態の推定精度を表す Fisher 情報量を用いて誤差
 や擾乱
や擾乱
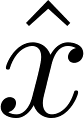 が定式化出来ることを示し、全ての測定過程が
が定式化出来ることを示し、全ての測定過程が
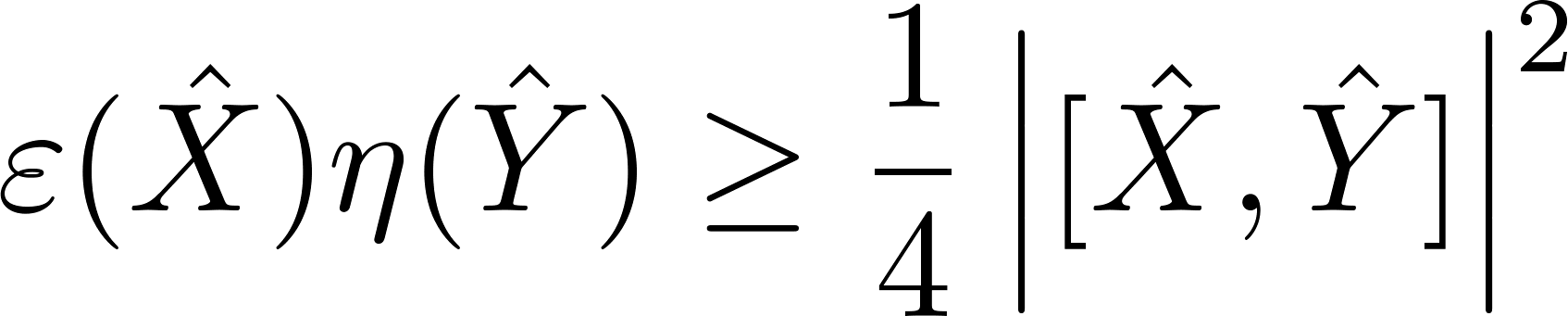 を満たすことを示した。したがって、これまでに広く信じられてきた Heisenberg の不確定性関係がたしかに
成り立つという事が明らかになった。しかしながら、この不等式は等号を達成する測定が常に存在するとは限
らず、交換関係は誤差と擾乱の下限を表す量としては緩いものになっている。そこで我々は、等号達成可能な
測定が常に存在する、より厳しい不等式として
を満たすことを示した。したがって、これまでに広く信じられてきた Heisenberg の不確定性関係がたしかに
成り立つという事が明らかになった。しかしながら、この不等式は等号を達成する測定が常に存在するとは限
らず、交換関係は誤差と擾乱の下限を表す量としては緩いものになっている。そこで我々は、等号達成可能な
測定が常に存在する、より厳しい不等式として
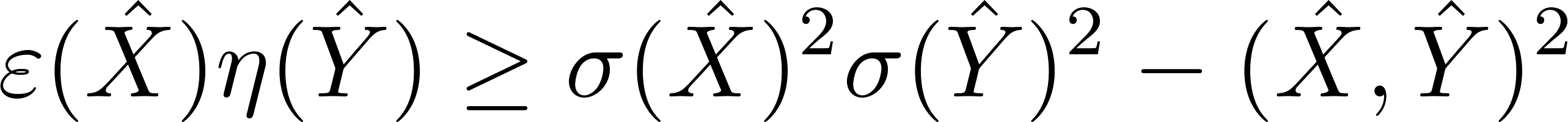 を示した。ここで、
を示した。ここで、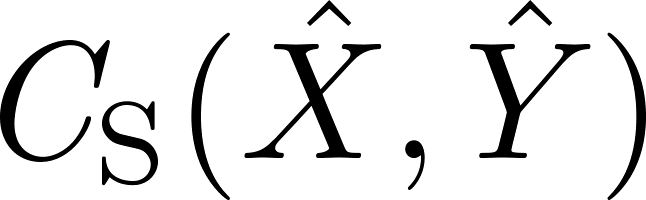 は
は
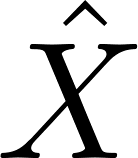 と
と
 の相関関数である。(ここでは
の相関関数である。(ここでは
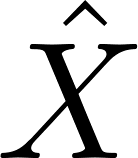 と
と
 の
の同時不変部分空間がヒルベ
ルト空間全体の場合のみを記した。一般には少し複雑になるので割愛する。) この不等式によって、測定に
よって量子系について我々が得ることの出来る知識の上限が明らかになった。現在、この不等式の実験への応
用について研究を行なっている。
なお、これらの研究結果により、渡辺優助教は 2012 年度東京大学理学系研究科研究奨励賞ならびに第 7 回
(2013 年) 日本物理学会若手奨励賞 (領域 1) を受賞した。
の
の同時不変部分空間がヒルベ
ルト空間全体の場合のみを記した。一般には少し複雑になるので割愛する。) この不等式によって、測定に
よって量子系について我々が得ることの出来る知識の上限が明らかになった。現在、この不等式の実験への応
用について研究を行なっている。
なお、これらの研究結果により、渡辺優助教は 2012 年度東京大学理学系研究科研究奨励賞ならびに第 7 回
(2013 年) 日本物理学会若手奨励賞 (領域 1) を受賞した。
参考文献
[1] Y. Watanabe, T. Sagawa, M. Ueda, Phys. Rev. A 84, 042121 (2011).
[2] Y. Watanabe, M. Ueda, arXiv:1106.2526 (2011).



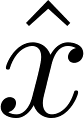 の測定誤差
の測定誤差
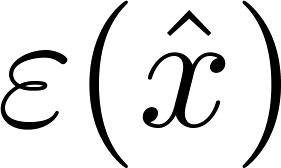 と測定による運動量
と測定による運動量
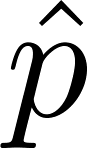 への擾乱
への擾乱
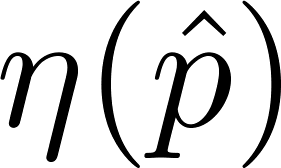 の間にトレードオフ関係
の間にトレードオフ関係
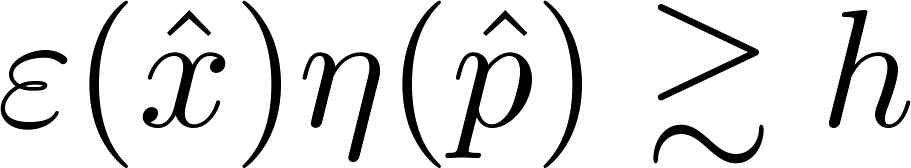 を見出した。このトレードオフ関係によって、ある物理量の測定をそれと共役な物理量への擾乱無しに行うことはできない、
という量子測定の相補性 (complementarity) が示唆された。
しかし、当時、量子測定についての理論はまだ完成していなかったため、
ガンマ線顕微鏡に限らない一般の測定過程における誤差と擾乱の間のトレードオフ関係が明らかにすることはできなかった。
さらに、同時期に発見された Kennard およびRobertson らによる量子揺らぎについてのトレードオフ関係
を見出した。このトレードオフ関係によって、ある物理量の測定をそれと共役な物理量への擾乱無しに行うことはできない、
という量子測定の相補性 (complementarity) が示唆された。
しかし、当時、量子測定についての理論はまだ完成していなかったため、
ガンマ線顕微鏡に限らない一般の測定過程における誤差と擾乱の間のトレードオフ関係が明らかにすることはできなかった。
さらに、同時期に発見された Kennard およびRobertson らによる量子揺らぎについてのトレードオフ関係
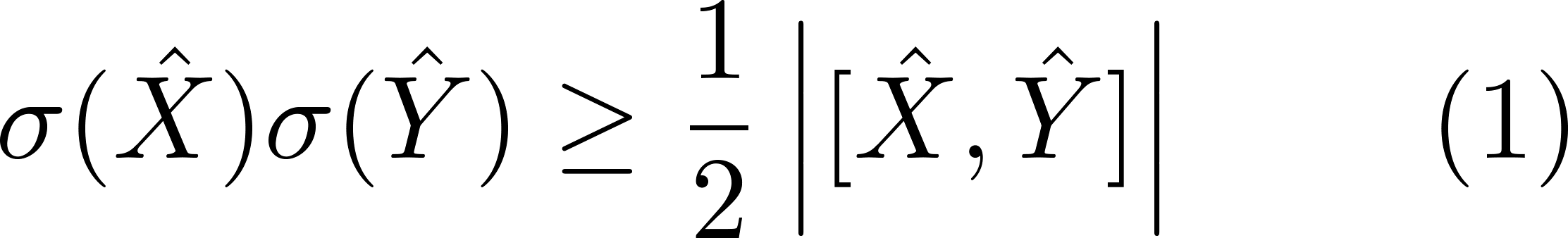 が Heisenberg の不確定性関係の数学的定式化であると誤って認識された。
しかしながら、量子揺らぎそのものは測定過程に依存せず、系に内在的な量であり、
したがって Robertson-Kennard の不等式は量子測定の誤差についてのトレードオフ関係ではない。
Robertson-Kennard の不等式に代表される、測定過程に依存しない、
対象となる量子系そのものの性質のみで表される不確定性関係は量子状態の非決定性 (indeterminacy) と呼ばれる。
近年の量子制御技術の発展によって、量子系に対する精密な測定が実現できるようになってきており、
量子測定の精度の限界を与える Heisenberg の不確定性関係が再び着目されるようになってきている。
これまで、量子測定の誤差は測定値の分散によって議論されてきた。しかし、測定値の分散が小さくても、
測定によって得られた情報量が多いとは一般に言えず、測定値の分散それ自身は測定の精度を表す指標にはな
らない。量子測定の相補性は、測定値の分散についてのトレードオフ関係ではなく、測定によって得られる互
いに非可換な物理量についての情報量の間にトレードオフ関係が存在することを示している。1970 年頃、量
子測定理論が Kraus や Davies らによって構築される一方、Helstrom や Holevo らによって量子推定理論の
基礎が研究された。量子推定理論は、例えば、未知の量子状態が与えられた場合、どのような測定を行えば量
子状態を効率よく推定できるかを明らかにする。推定精度が高いほど量子測定によって得られる情報量は多
く、逆に推定精度が低い場合には測定によって得られる情報量は少ない。したがって、現代的な観点からは、
Heisenberg の不確定性関係は測定によって得られたある物理量についての情報量と、測定過程による反作用
が引き起こす共役な物理量についての情報の損失の間のトレードオフ関係として捉えられる。
我々は、測定結果からの量子状態の推定精度を表す Fisher 情報量を用いて誤差
が Heisenberg の不確定性関係の数学的定式化であると誤って認識された。
しかしながら、量子揺らぎそのものは測定過程に依存せず、系に内在的な量であり、
したがって Robertson-Kennard の不等式は量子測定の誤差についてのトレードオフ関係ではない。
Robertson-Kennard の不等式に代表される、測定過程に依存しない、
対象となる量子系そのものの性質のみで表される不確定性関係は量子状態の非決定性 (indeterminacy) と呼ばれる。
近年の量子制御技術の発展によって、量子系に対する精密な測定が実現できるようになってきており、
量子測定の精度の限界を与える Heisenberg の不確定性関係が再び着目されるようになってきている。
これまで、量子測定の誤差は測定値の分散によって議論されてきた。しかし、測定値の分散が小さくても、
測定によって得られた情報量が多いとは一般に言えず、測定値の分散それ自身は測定の精度を表す指標にはな
らない。量子測定の相補性は、測定値の分散についてのトレードオフ関係ではなく、測定によって得られる互
いに非可換な物理量についての情報量の間にトレードオフ関係が存在することを示している。1970 年頃、量
子測定理論が Kraus や Davies らによって構築される一方、Helstrom や Holevo らによって量子推定理論の
基礎が研究された。量子推定理論は、例えば、未知の量子状態が与えられた場合、どのような測定を行えば量
子状態を効率よく推定できるかを明らかにする。推定精度が高いほど量子測定によって得られる情報量は多
く、逆に推定精度が低い場合には測定によって得られる情報量は少ない。したがって、現代的な観点からは、
Heisenberg の不確定性関係は測定によって得られたある物理量についての情報量と、測定過程による反作用
が引き起こす共役な物理量についての情報の損失の間のトレードオフ関係として捉えられる。
我々は、測定結果からの量子状態の推定精度を表す Fisher 情報量を用いて誤差
 や擾乱
や擾乱
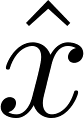 が定式化出来ることを示し、全ての測定過程が
が定式化出来ることを示し、全ての測定過程が
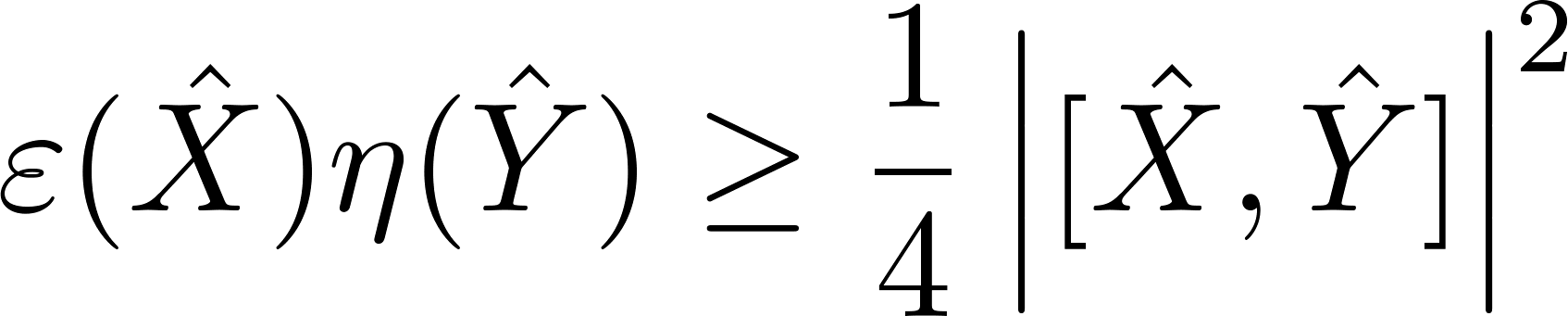 を満たすことを示した。したがって、これまでに広く信じられてきた Heisenberg の不確定性関係がたしかに
成り立つという事が明らかになった。しかしながら、この不等式は等号を達成する測定が常に存在するとは限
らず、交換関係は誤差と擾乱の下限を表す量としては緩いものになっている。そこで我々は、等号達成可能な
測定が常に存在する、より厳しい不等式として
を満たすことを示した。したがって、これまでに広く信じられてきた Heisenberg の不確定性関係がたしかに
成り立つという事が明らかになった。しかしながら、この不等式は等号を達成する測定が常に存在するとは限
らず、交換関係は誤差と擾乱の下限を表す量としては緩いものになっている。そこで我々は、等号達成可能な
測定が常に存在する、より厳しい不等式として
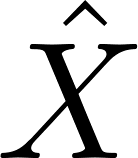 と
と
 の相関関数である。(ここでは
の相関関数である。(ここでは
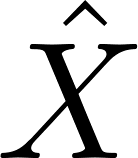 と
と
 の
の同時不変部分空間がヒルベ
ルト空間全体の場合のみを記した。一般には少し複雑になるので割愛する。) この不等式によって、測定に
よって量子系について我々が得ることの出来る知識の上限が明らかになった。現在、この不等式の実験への応
用について研究を行なっている。
なお、これらの研究結果により、渡辺優助教は 2012 年度東京大学理学系研究科研究奨励賞ならびに第 7 回
(2013 年) 日本物理学会若手奨励賞 (領域 1) を受賞した。
の
の同時不変部分空間がヒルベ
ルト空間全体の場合のみを記した。一般には少し複雑になるので割愛する。) この不等式によって、測定に
よって量子系について我々が得ることの出来る知識の上限が明らかになった。現在、この不等式の実験への応
用について研究を行なっている。
なお、これらの研究結果により、渡辺優助教は 2012 年度東京大学理学系研究科研究奨励賞ならびに第 7 回
(2013 年) 日本物理学会若手奨励賞 (領域 1) を受賞した。