概要

Siのフォノンを例に、状態密度と分散の計算を行う。これらの計算には任意の波数におけるフォノンの情報が必要であるので、事前に実空間におけるdynamical matrixの計算を行う必要がある。

準備

電子状態計算

Si.scf.in

&control
  calculation = 'scf',
  prefix      = 'Si'
  pseudo_dir  = './pseudo',
  outdir      = './tmp/'
/
&system
  ibrav     = 2,
  celldm(1) = 10.2656,
  nat       = 2,
  ntyp      = 1,
  ecutwfc   = 50.0
/
&electrons
  conv_thr = 1.0d-12
/
ATOMIC_SPECIES
 Si  28.0855  Si.pbesol-n-kjpaw_psl.1.0.0.UPF
ATOMIC_POSITIONS (alat)
 Si 0.00 0.00 0.00
 Si 0.25 0.25 0.25
K_POINTS automatic
 8 8 8 1 1 1

$ pw.x < Si.scf.in > Si.scf.out

dynamical matrixの計算

Si.ph.in

phonons of Si
&inputph
  tr2_ph = 1.0d-14,
  prefix = 'Si',
  outdir = './tmp/',
  fildyn = 'Si.dyn',
  ldisp  = .true.,
  nq1    = 4,
  nq2    = 4,
  nq3    = 4,
/

変数	説明
ldisp	.true.とした場合、波数空間を指定したメッシュ数に区切り、その点におけるフォノンの固有振動数を求める。
nq1,nq2,nq3	x,y,z方向のメッシュの数

実行は次のようにします。

$ ph.x < Si.ph.in > Si.ph.out

フォノンの計算には時間がかかるので、メッシュのとりすぎに注意します。ただし、メッシュの数による収束は必ず確認すること。

実空間へのフーリエ変換

q2r.xというプログラムを使って、dynamical matrixを波数空間から実空間に変換する。次のファイルを用意する。

Si.q2r.in

&input
  fildyn = 'Si.dyn'
  flfrc = 'Si.fc'
/

fildynにはさきほど用意した波数空間のdynamical matrixの出力ファイルを指定する。出力先はSi.fcになる。実行は次のようにする。

$ q2r.x < Si.q2r.in > Si.q2r.out

以上で準備は終了である。

フォノンの状態密度と分散

状態密度

次の入力ファイルを用意する。

Si.matdyn.phdos.in

&input
  flfrc = 'Si.fc'
  fldos = 'Si.phdos'
  asr = 'crystal'
  dos = .true.
  nk1 = 16,
  nk2 = 16,
  nk3 = 16,
/

変数	説明
flfrc	さきほど作成した実空間のdynamical matrixを指定する
fldos	出力ファイル名。
asr	acoustic sum ruleの略で、q=0で音響フォノンがゼロになるように指定している。実は数値誤差の関係で音響フォノンはq=0でもゼロになってくれない。また、一次元系ではasr = 'one-dim'とする。
dos	状態密度を計算する。
nk1,nk2,nk3	状態密度を計算するときのメッシュの数。

詳しくはmatdyn.f90の先頭にあるコメントを参照のこと。

実行は次のようにする。

$ matdyn.x < Si.matdyn.phdos.in > Si.matdyn.phdos.out

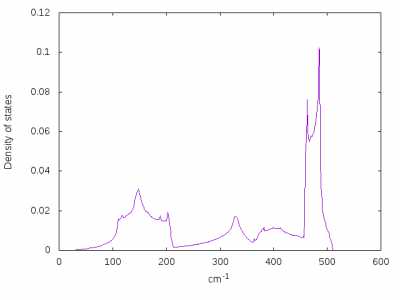
下図は Si.phdos に出力されたデータをプロットした。

分散

分散の場合は計算する波数点の経路（デカルト座標で、単位は格子定数aを使って2π/a）を指定する。

Si.matdyn.freq.in

&input
  asr = 'crystal'
  flfrc = 'Si.fc'
  flfrq = 'Si.freq'
  q_in_band_form=.true.
/
3
0.5 0.5 0.5  20
0.0 0.0 0.0  20
1.0 0.0 0.0  1

変数	説明
flfrq	出力するファイル名
q_in_band_form	バンドの経路を指定。もしも.false.ならすべての波数点を列挙する。

実行はさきほどと同様。

$ matdyn.x < Si.matdyn.freq.in > Si.matdyn.freq.out

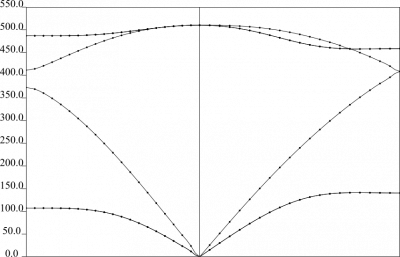
結果はSi.freqに出力される。分散はplotband.xでプロットできる。

$ plotband.x
Input file > Si.freq
Reading 6 bands at 41 k-points
Range: 0.0000 510.2482eV Emin, Emax > 0, 550
high-symmetry point: 0.5000 0.5000 0.5000 x coordinate 0.0000
high-symmetry point: 0.0000 0.0000 0.0000 x coordinate 0.8660
high-symmetry point: 1.0000 0.0000 0.0000 x coordinate 1.8660
output file (gnuplot/xmgr) > freq.xmgr
bands in gnuplot/xmgr format written to file freq.xmgr
output file (ps) > freq.ps
Efermi > 0
deltaE, reference E (for tics) 50,0
bands in PostScript? format written to file freq.ps

なお、縦軸の単位はcm^{-1}である。

GNUPLOTでプロットしたい場合は Si.freq.gp に出力されているものを使うと便利です。

固有振動モードの可視化

Phonon websiteを使えば、フォノンの各エネルギーに対応する固有振動モードを可視化することができます。

ホームディレクトリに戻り、Githubから必要なソフトをダウンロードします

$ cd
$ git clone https://github.com/henriquemiranda/phononwebsite

インストールします

$ cd phononwebsite
$ python setup.py install --user

フォノン計算の作業ディレクトリに入り、SCF計算の入力ファイルをprefix.scf、フォノン分散の計算で得られたmatdyn.modesをprefix.modesという名前にコピーします。 prefixの部分はなんでも良いです。

結晶の基本並進ベクトル CELL_PARAMETERS を指定している場合は、ボーア半径で指定してください。
原子位置 (ATOMIC_POSITIONS) は分率座標 (crystal) で指定してください。

そして次のコマンドを実行します。

$ read_qe_phonon.py prefix

すると prefix.json というファイルが得られます。

さきほどダウンロードしたディレクトリの中にある phononwebsite/phonon.html か、あるいは https://henriquemiranda.github.io/phononwebsite/phonon.html を開き、Custom file の [Browse] で prefix.json を開きます。

エネルギー分散をクリックすることで、そのエネルギーに対応する固有振動モードのアニメーションを見ることができます
振動のアニメーションを保存したい場合は Export movie の [gif] をクリックすると録画が開始します。

注意

構造が不安定な系では、対応するモードのフォノンの振動数が複素数になります（出力ファイルは負の振動数で表現されます）。これは簡単にはフォノンのバネ定数が負になってしまう（つまり変形したほうがエネルギー的に安定）ことに対応します。

Table of Contents

概要

準備