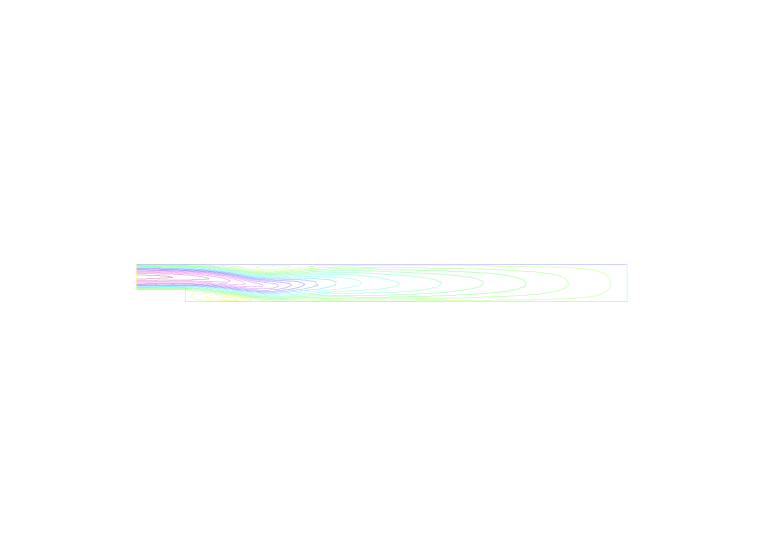
FreeFEM++ 例題3-7: Chorin法による非圧縮NS方程式 (MAC法に似ている?)
a1
a2
a3


ラベル2 (a1+a2+a3)
ラベル1 (a0)
ラベル3 (a4)
ラベル4 (a5)
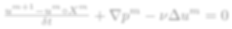
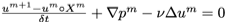

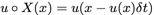

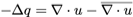

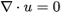

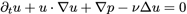
Chorinアルゴリズムを用いると
RannacherによるChorinアルゴリズムの改良版では重み関数に関し

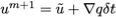
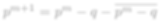
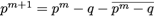
計算部分
real area= int2d(Th)(1.); //面積全体Ω
Vh uold = u, vold = v, pold=p; //流速u,v圧力p
Vh f=convect([u,v],-dt,uold), g=convect([u,v],-dt,vold); //移流項f,gとする。
solve pb4u(u,w,init=n,solver=LU)
=int2d(Th)((u-f)*w/dt + dx(p)*w +nu*(dx(u)*dx(w)+dy(u)*dy(w)))
+ on(1,u = 4*y*(1-y)) + on(2,4,u = 0)+ on(3,u=f); //境界条件
solve pb4v(v,w,init=n,solver=LU)
= int2d(Th)((v-g)*w/dt + dy(p)*w +nu*(dx(v)*dx(w)+dy(v)*dy(w)))
+on(1,2,3,4,v = 0); //境界条件
real meandiv = int2d(Th)(dx(u)+dy(v))/area; //uのdivの平均
solve pb4p(q,w,init=n,solver=LU)= int2d(Th)(dx(q)*dx(w)+dy(q)*dy(w))
- int2d(Th)((dx(u)+ dy(v)-meandiv)*w/dt)
+ on(3,q=0); //境界条件
real meanpq = int2d(Th)(pold - q)/area; //pold-qの平均
p = pold-q-meanpq;
u = u + dx(q)*dt;
v = v + dy(q)*dt;
ただし移流項に関しては以下で表す
とし、m+1での流速と圧力を

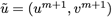
ただし、
非圧縮NS方程式
つまり
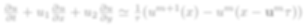
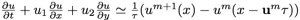
流速u