配布プリント 配布プリント
Lesson01 (実数の和)
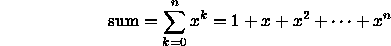
このプログラムでは、より一般的な DO ループの形式を使っています。
(例) k = n から 0 まで一つずつへらして繰り返す場合。
きざみを省略すると、1 と見なされます。(K が 1 ずつ増える)
Lesson02 (数値積分 その1)
| 関数名 | 数式 | 意味 |
|---|---|---|
| sqrt(x) | x1/2 | 平方根 |
| exp(x) | ex | 指数関数 |
| log(x) | logex | 自然対数 |
| log10(x) | log10x | 常用対数 |
| sin(x) | sin(x) | 正弦関数 |
| cos(x) | cos(x) | 余弦関数 |
| tan(x) | tan(x) | 正接関数 |
| asin(x) | sin-1(x) | 逆正弦関数 |
| acos(x) | cos-1(x) | 逆余弦関数 |
| atan(x) | tan-1(x) | 逆正接関数 |
| atan2(x,y) | tan-1(y/x) | 逆正接関数 |
| sinh(x) | sinh(x) | 双曲正弦関数 |
| cosh(x) | cosh(x) | 双曲余弦関数 |
| tanh(x) | tanh(x) | 双曲正接関数 |
| abs(x) | |x| | 絶対値 |
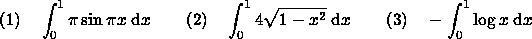
これらのプログラムは (ex0211.f 以外は) あまり精度が高くありません。 端点に特異性がある場合の扱いは、 例えば今週 (lesson03) 余裕があればやってみよう のところで取り扱っていますが、時間が無いかも知れません。
上の右に載せてある 3 つのプログラムは高精度の積分を行なうように 書かれています。(誤差が 10-15程度になると本当の足し算の誤差です。)
Lesson03
(数値積分 その2)
Lesson04
(微分方程式 その 1, 1 変数 1 階の微分方程式)
Lesson05
(微分方程式 その 2, 1 変数 2 階の微分方程式)
ファイルから入力して実行・ファイルに出力して、グラフを描くコマンドは次の通り
ap1: f90 ex05X.f
ap1: a.out < ex05X.in > ex05X.dat
ap1: gnuplot ex05X.plt
ここで X は、1,2,3 のいずれかです。
Lesson06
(微分方程式 その 3, ケプラー問題, 2 変数 2 階の微分方程式)
ap1: f90 ex061.f
ap1: a.out < ex061.in > ex061.dat
ap1: gnuplot ex061.plt
ap1: f90 ex062.f
ap1: a.out < ex062.in > ex062.dat
ap1: gnuplot ex062.plt
Lesson07 (一般の方程式, 2分法と Newton 法)
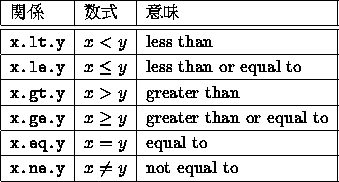
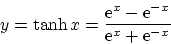の逆関数
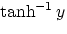
ap1: f90 ex071.f
ap1: a.out > ex071.dat
ap1: gnuplot ex071.plt
ap1: f90 ex072.f
ap1: a.out < ex0721.in > ex0721.dat
ap1: a.out < ex0722.in > ex0722.dat
ap1: gnuplot ex072.plt
Lesson08 (課題 その2)
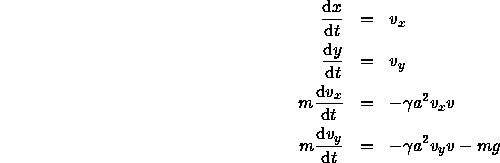
前回の問題設定のもとに、 v0=30, a = 0.2, m = 1, γ = 1 として、 到達距離を最大にする仰角 θ を有効数字 ３桁まで求めて下さい。 単位はdegreeでお願いします。
Lesson09 (乱数 その1)
Lesson10 (乱数 その2)
