● Lesson04 (微分方程式 その1, １変数１階微分方程式)

• 今週、最初にやること
• 今週の PROGRAM
• 今日のポイント
• グラフを描いてみよう
• 演習問題
• プログラムができたら...

● 今週最初にやること

• Routine works:
  • 出席メールの受け取り状況のページ の確認
  • directory にファイルをまとめる。
• Lesson02 の演習問題の答え を公開しています。
• 先週の演習での代表的な質問 にたいするコメント もみておいて下さい。
• 中点公式での誤差についての ノートをまとめました。
• 課題の採点はまだです。
• 今週の Unix の練習は gnuplot でグラフを描く練習です。 プログラムを書いてからにします。

今週の最初へ戻る

● 今週の PROGRAM

区分数 n を入力して、 初期条件 y(1)=1 のもとに、 次の微分方程式を解くプログラムをつくって下さい。 もちろん答えは 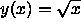です。

• オイラー法で微分方程式を解くプログラム (計算実行例)

  このプログラムでは、差分法を使って次のように解いています。

  

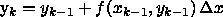
  本当の"仕事" をしているのは 26 行目

           y = y + dy        ! y(k) = y(k-1) + dx * f(x(k-1), y(k-1))
  

  だけですね。

今週の最初へ戻る

● 今日のポイント

• 常微分方程式の(解析的な)解き方
  1. 変数分離形

     

  2. 同次形 ... u=y/x と置き換えて変数分離形へ

     

  3. 1階線形常微分方程式
     
     ... 一般解 = 特解 + 同次方程式の一般解

     

     

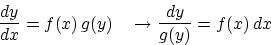
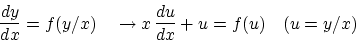
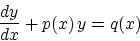
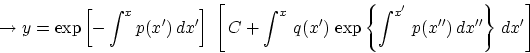
     (C は積分定数)

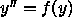     の形 ... u=dy/dx とおくと変数分離形へ

     

• 常微分方程式の(数値的な)解き方
  1. オイラー法:

     

  2. 修正オイラー法: 半分進ませた点での微係数を使う。

     

  3. 改良オイラー法
  4. Heun の公式

• open(unit, file='filename')
  例えば、write(16,*) .... として、prog04.dat に書き出したい場合、

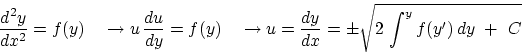
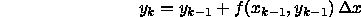
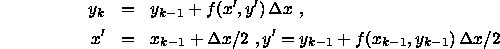
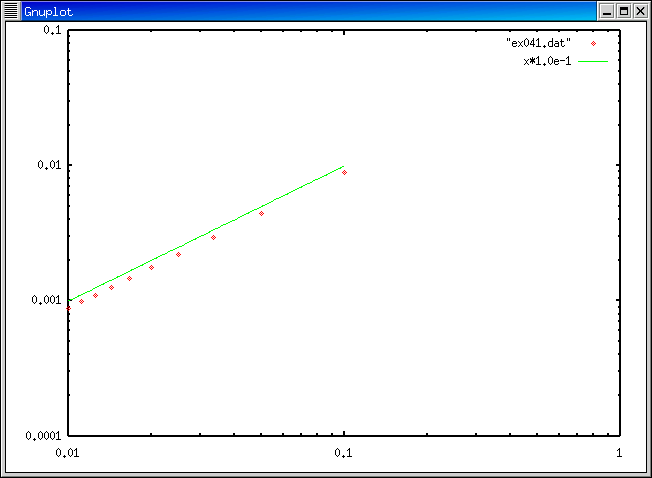
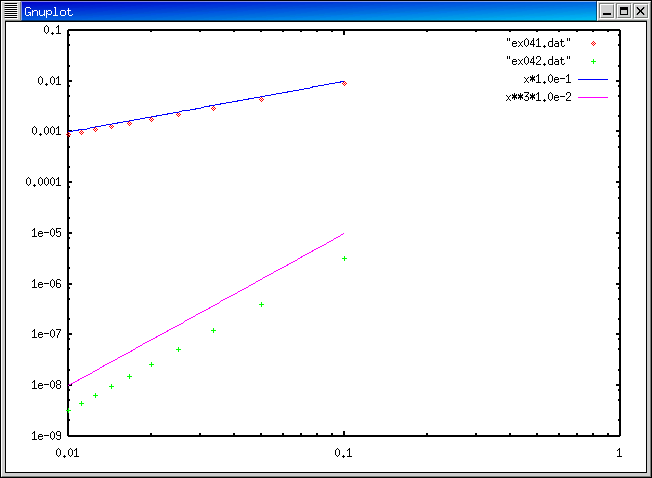
  	open(16,file='prog04.dat')
  

  とすればよい。

今週の最初へ戻る

● グラフを描いてみよう

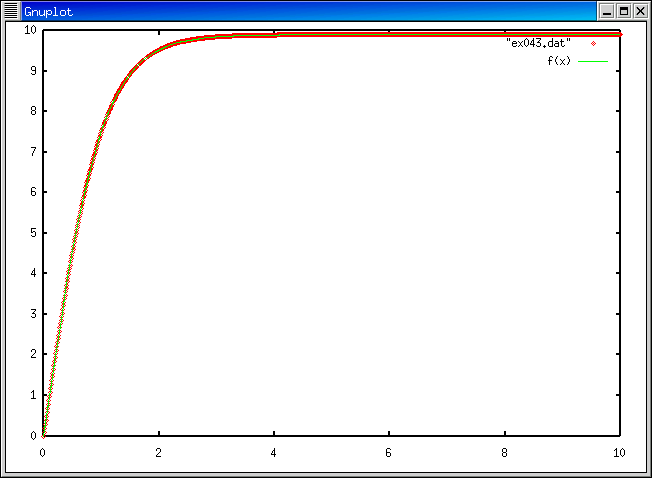
今週は gnuplot というコマンドを使って、 グラフを描いてみましょう。 やりかたは ここ 。

今週の最初へ戻る

● 演習問題

1. 今回のプログラムで 刻み幅 dx を小さくする（ n を大きくする）と、 どのように真の値に近付くかを確かめてみよう。 x=2 の時の近似値と真の値の差を dx の関数としてプロットするのに 便利なデータを出力するように改造し、 その様子を調べて下さい。
   
   • Example Program (ex041.f)
   • Gnuplot Script (ex041.plt)
   

2. 上で改造したプログラムを修正オイラー法を用いるものに変更し、 どの程度改良されるかを調べてみよう。
   
   • Example Program (ex042.f)
   • Gnuplot Script (ex042.plt)
   

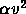3. 空気中を速さvで落下する物体には、 空気抵抗の力が働くものとします。このとき、 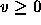とすれば、重力加速度gのもとで落下する物体の運動方程式は

   

   となります。 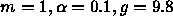として 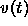を求めるプログラムを作ってみよう。 ただし初期条件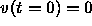とします。
   

   • Example Program (ex043.f)
   • Gnuplot Script (ex043.plt)
   

• f90 xxx.f
• a.out
• gnuplot xxx.plt