|compphys|
( のマークは必須!)
のマークは必須!)
今週の最初へ戻る
今週は「簡単には解析的に解けない」微分方程式を解いてみましょう。
振り子の問題です。
区分数
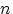 を入力して、初期条件
を入力して、初期条件
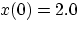 ,
, 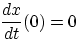 のもとに、
のもとに、
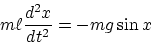
を、時刻 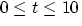 において、改良オイラー法で解き、
各時刻 t における位置(実際は角度) x、速度(実際は角速度) v、
エネルギー E を出力するプログラムを作りましょう。
ただし、
において、改良オイラー法で解き、
各時刻 t における位置(実際は角度) x、速度(実際は角速度) v、
エネルギー E を出力するプログラムを作りましょう。
ただし、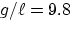 として下さい。
として下さい。
このプログラムでは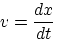 とおいて、
とおいて、
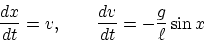
と変形し、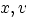 を連立して解いています。
を連立して解いています。
1変数2階微分方程式を改良オイラー法でとくプログラム (prog05.f)
今週の最初へ戻る
- 2階常微分方程式は、2変数の1階常微分方程式へ。
- 常微分方程式の(数値的な)解き方
- オイラー法
- 修正オイラー法
- 改良オイラー法: オイラー法で進ませた点での微係数との平均
- Heun の公式
今週の最初へ戻る
プログラムができたら、ファイルから入力して計算を実行し、
計算結果をファイルに出力してグラフを描いてみましょう。
やり方は ここ。
今週の最初へ戻る
まずは、頑張って自分で解いてみて下さい。
つまずいたら、Example Program をみてヒントを探しましょう。
-
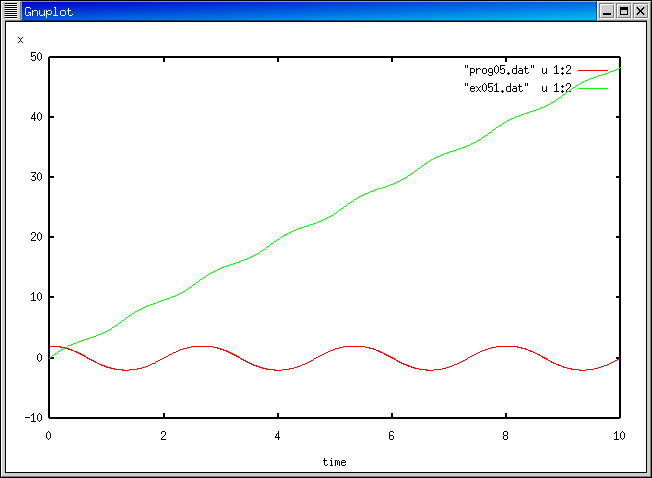
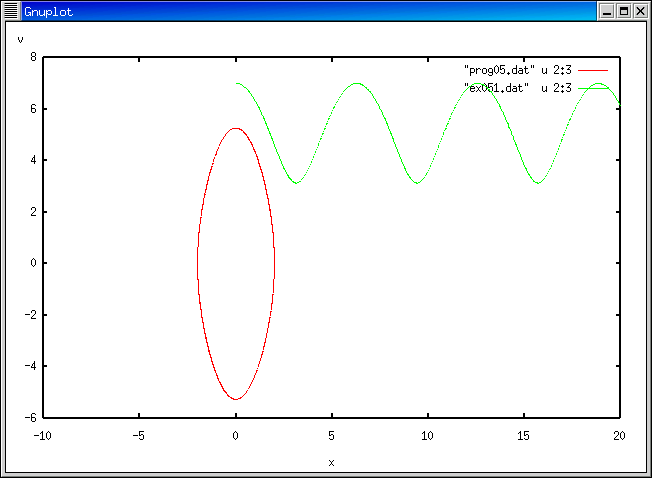
今回のプログラムの結果はグラフに描けましたか。
いろいろな初期条件でプログラムを走らせてみよう。
また、どの程度エネルギーが保存されているか確かめてみよう。
ファイル名は ex051.f として下さい。
振動の状態と回転の状態
-
次の2階微分方程式を解くプログラムを作ってみよう。
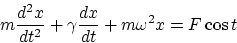
どっかでみたことある方程式ですね。
m=F=1 として、
初期条件と ω, γ を
いろいろ変えて解いた結果をグラフに描いてみよう。
力学で勉強したような答えになりましたか。
ファイル名は ex052.f として下さい。
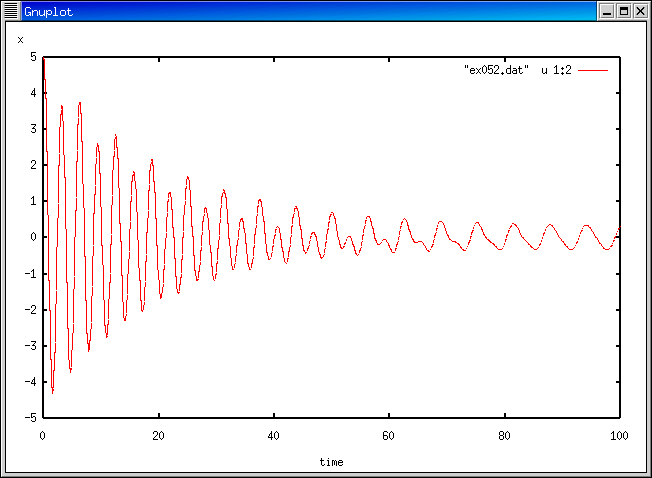
gam=0.1, omg=2.0 (減衰振動)
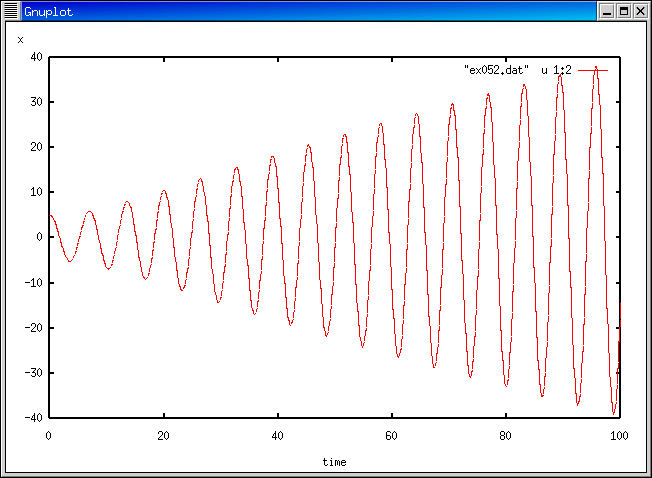
gam=0.01, omg=1.0 (共振)
-
2 で作ったプログラムを、サブルーチンを使って書き換えてみよう。
位置 x, 速度 v, 時刻 t, 微小時間 dt,
摩擦係数 gam, 固有振動数 omg を与えて、
1段階の時間発展を求めるサブルーチン、
- subroutine impeul(x,v,t,dt,gam,omg)
を作り、これを使って上の微分方程式を作るプログラムを作って下さい。
ファイル名は ex053.f として下さい。
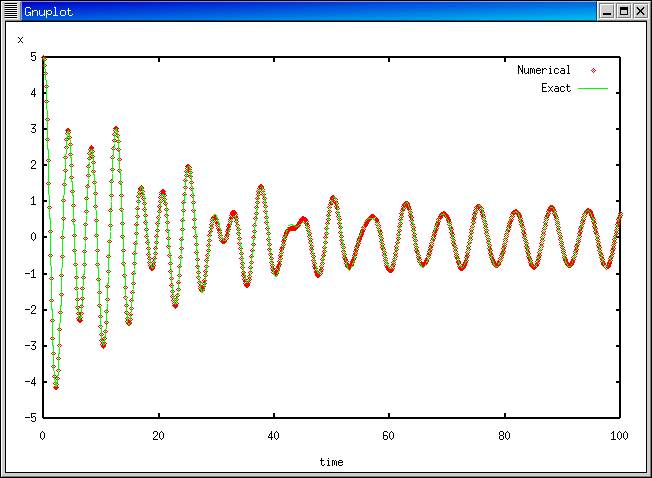
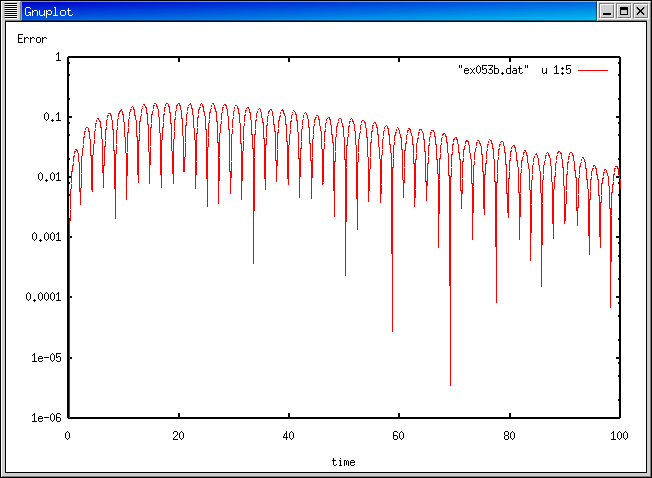
参考: 厳密解と比較する Program (ex053b.f)
今週の最初へ戻る
出席の返事の代わりに、
 mail Teacher@server s0300xyz < prog05.f
mail Teacher@server s0300xyz < prog05.f
として、プログラムを送って下さい。
今週の最初へ戻る



 のマークは必須!)
のマークは必須!)

![]() を入力して、初期条件
を入力して、初期条件
![]() ,
, 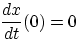 のもとに、
のもとに、
![]()
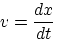 とおいて、
とおいて、
![]()
![]()


![]()
 mail Teacher@server s0300xyz < prog05.f
mail Teacher@server s0300xyz < prog05.f