

(皆さんのグラフのページ)
(皆さんのグラフのページ)






 のマークは必須!)
のマークは必須!)


課題の問題設定
空気抵抗を考慮した大砲の砲撃の問題を考えます。水平方向、垂直方向を それぞれ x , y 方向とします。 仰角 θ で大砲を初速度の大きさ v0 で打ち出すとき、 弾の運動方程式は
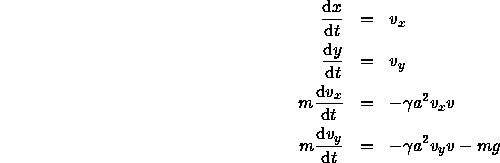
となるとします。
ここで、γ は定数、 a と m は弾の半径と質量で、 v は速度の大きさ
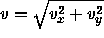 です。
初期条件は
です。
初期条件は
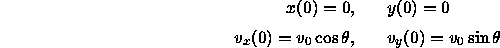
で与えられます。
例えば、
θ = π/4,
v0 = 20,
a = 0.1,
γ = 1
としてプログラムを走らせると、
弾の軌跡はどのようになりますか。
グラフを描いて確かめて下さい。
また、γ = 0 としたとき、放物線になりますか? グラフを描いて確かめて下さい。

前回の問題設定のもとに、 v0=30, a = 0.2, m = 1, γ = 1 として、 到達距離を最大にする仰角 θ を有効数字 3桁まで求めて下さい。 単位はdegreeでお願いします。
あなたの作った 「最終的なプログラム」 と 「最終的な答え」、 そして 「その答をどのように求めたか」 をまとめてメールして下さい。
できたところまでで構いません。
最後まで出来なかった人はどこまで出来たかの詳細を書いてメイルして下さい。
締め切りは1月23日(必着)とします。
時間発展 (課題設定の 1.) の部分は、 prog06.f を もとにして考えると分かりやすい。 subroutine onestep, subroutine force を作って おくと後々便利である。
上のプログラムで y < 0 となった最初の時間 t = t1 は分かるので、 そのあたりから時間を少しもどせばよいだろう。 求めるのは x = xf だが、時間を媒介にして行なうのがよいと思われる。 もどす時間のステップは、例えば、Newton 法で求められる。
当然ながら、前に作った subroutine はそのまま使える。
(prog081.f のサブルーチン onestep, force を加えることが必要)
まず、 「θ をあたえて xf を返す subroutine」
をつくっておくとよい。 これは、大雑把にいえば prog082.f のメイン・プログラムを subroutine にしたもの といえる。 プログラムの構成としては、 メイン・プログラムで do loop により θ を次々と変化させて 上の subroutine solvexf を call すればよい。 再び、当然ながら前に作った subroutine (onestep, force, solvey0) はそのまま使える。
(prog081.f のサブルーチン onestep, force、 prog082.f のサブルーチン solvey0、を加えることが必要)
おそらく 10。 < θ < 90。 の範囲内で xf は最大に なるだろう。よって、「有効数字3桁」ということは、θの誤差が Δθ < 0.1。であればよい。 より具体的には、0.01。 単位で xf が最大となる θ をさがして、四捨五入すれば答えは求まる。
プログラムの構成としては、
再び、当然ながら前に作った subroutine はそのまま使える。
今週の内容は「課題の途中まで」なので、中間報告のプログラムの
メールは必要ありません。
(来週と冬休みで頑張って作って下さい。"一発勝負"で提出してもらいます。)
ただし、出席確認のために
質問・コメントをメールして下さい。
方法は問いません。
mule から、
あるいは PC からメールして下さい。
