積分の可視化の例

関数の積分は、関数と x 軸で囲まれた面積で与えられます。これは、領域を N 個に分割して、その中点での値に短冊の幅 $\Delta x = (b-a)/N$ を掛けて足し合わせ、 $N \to \infty$ の極限をとったものとしても表せます。

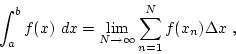
$\begin{displaymath} \int_a^b f(x)\ dx = \lim_{N \to \infty} \sum_{n=1}^N f(x_n) \Delta x \ ,\end{displaymath}$

$\begin{displaymath} x_n = a + \Delta x \ (n - {1\over 2})\end{displaymath}$

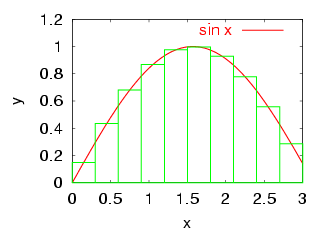
さて、下のグラフでは [0,3] の区間を 10 分割して $\sin x$ の積分を短冊の面積の和と比べています。関数の値と分割した区間の中点の値は異なっていますが、上下の差が大体打ち消していることが分かりますね。この場合には、結果として

関数の積分値 = 1.9899925

短冊の面積の和 = 1.9974746

となっており、有効数字2桁程度で一致しています。

Akira OHNISHI
10/25/2001