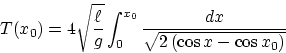教職コース
, 続きのページ
6. 単振り子の問題
今回と次回で、再び図を載せたプリントを作りましょう。
ただし、そろそろ「物理の問題」に入ります。
- 下記の問題設定のもとで、単振り子の周期を求めるプログラムを作って下さい。
-
このプログラムを使って、
周期が近似値
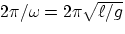 からどの程度ずれるか、グラフで示して下さい。
からどの程度ずれるか、グラフで示して下さい。
- 課題提出(連絡)は次回の プリントへのリンクをつけた Webpage と
まとめて行ってもらいます。
● 問題設定 (単振り子)
今回扱うのは単振り子です。
長さ 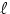 の質量が無視できるたるまない糸の先につけた
質量 m の質点の運動を考えます。
垂線からの振り子の角度を x (rad.) とすると、
運動方程式は
の質量が無視できるたるまない糸の先につけた
質量 m の質点の運動を考えます。
垂線からの振り子の角度を x (rad.) とすると、
運動方程式は
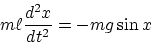
となります。
高校では小さい角度のみを考え、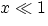 として
として
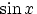 の近似式
の近似式
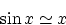
を使って運動方程式を簡単にします。
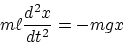
そうするとこれはバネ定数が 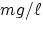 のバネ振り子と同じ
運動方程式になるので、次のように解くことが出来ます。
のバネ振り子と同じ
運動方程式になるので、次のように解くことが出来ます。
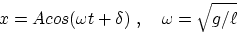
すなわち、糸の長さが等しければ最初の角度によらず
同じ周期の振動運動をするのです。
このことは歴史的にも重要な「発見」だったのですが、
皆さんは高校生のとき、
「この近似はどの程度正しいのだろうか ?」
と思ったことはありませんか ?
高校生のこうした疑問には、
「数値計算」を使って答えましょう。
これ以降、
初期条件が t=0 において x=x0 (>0), v=dx/dt=0 である場合を考えます。
また、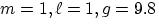 として下さい。
として下さい。
● Examples
● Hints
- グラフを書くためには
倍精度実数の出力で指数部を表す D (1.023D-01 など) は
gnuplot が理解できません。
単精度実数への変換関数 real(x) を用いて単精度の指数表示をしましょう。
- 単純な中点公式では x0 の小さいところで
周期が短くなっています。これは間違いなので、少なくとも少しは
精度を上げる必要があるでしょう。
ここから先は各自が工夫してみて下さい。
困ったら下の例を参考にして下さい。
教職コースの目次へ戻る
Akira OHNISHI
10/10/2002
 今回の課題
今回の課題
 今回の課題
今回の課題
![]() の質量が無視できるたるまない糸の先につけた
質量 m の質点の運動を考えます。
垂線からの振り子の角度を x (rad.) とすると、
運動方程式は
の質量が無視できるたるまない糸の先につけた
質量 m の質点の運動を考えます。
垂線からの振り子の角度を x (rad.) とすると、
運動方程式は
![]()
![]()
![]()
![]()
![]() として下さい。
として下さい。
![]()
![]() と近似した場合と比べて
大きくなりますか、それとも小さくなりますか ?
と近似した場合と比べて
大きくなりますか、それとも小さくなりますか ?