Title
Instabilities in Granular Shear Flows
Abstract
In this presentation, we show full details of our weakly nonlinear analysis of granular shear flows
and phenomenological models of cohesive powders under shear.
We divide the presentation into two parts: “I. Instabilities of dry granular particles under shear”
and “II. Instabilities of cohesive powders under shear”.
I. Instabilities of dry granular particles under shear
Though instabilities of dry granular particles under shear are governed by the shear rate
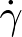
and the dissipation rate
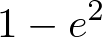
with the restitution coefficient
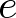
, they can be reduced to a small parameter
"
",
if we assume that mean granular temperature is
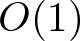
in the hydrodynamic limit.
We expand the hydrodynamic equations of granular gases in the series of
"
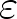
"
and obtain the lowest-order amplitude equation at the third order of
"
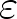
"
We develop the perturbative calculations to the fifth order of
"
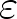
"
to derive the higher-order amplitude equations. From our analysis,
we find the supercritical bifurcations in dilute gases and the subcritical bifurcations in denser gases.
Because the most unstable mode is zero in the sheared direction,
any disturbances of the hydrodynamic fields in this direction will be suppressed within the long time scale
(
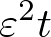
).
As a result, the amplitude equations are one-dimensional equations.
To obtain two-dimensional amplitude equations, we need to develop the usual procedures of weakly nonlinear analysis
by taking into account the contributions from the linearly stable modes.
The resultant amplitude equation can be written as
where
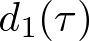
and
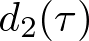
are time-dependent diffusion coefficients. Because
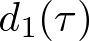
and
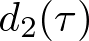
converge to zero,
Eq. (1) is reduced to the one-dimensional equation which is derived by the usual weakly nonlinear analysis [1].
Numerically solving Eq. (1), we confirm that the dynamics of granular shear flows are qualitatively explained
by the two-dimensional amplitude equation [2, 3].
II. Instabilities of cohesive powders under shear
In our molecular dynamics simulations of three-dimensional cohesive powders under shear,
we observe various shapes of aggregates, e.g. droplets, plugs, plates and etc [4].
To study the dynamics and instabilities, we modify the hydrodynamic equations for the Lennard-Jones liquids
to include the effect of interface and dissipation of energy.
We numerically solve the hydrodynamic equations and discuss the instabilities of cohesive powders [5].
[1] K. Saitoh and H. Hayakawa, Granular Matter 13 (2011) 697.
[2] K. Saitoh and H. Hayakawa, AIP Conf. Proc. 1501 (2012) 1001.
[3] K. Saitoh and H. Hayakawa, Phys. Fluids (2013) in press.
[4] S. Takada, K. Saitoh, and H. Hayakawa in preparation.
[5] K. Saitoh, S. Takada, and H. Hayakawa, in preparation.