京都大学 基礎物理学研究所 - 物性基礎論 - 凝縮系物理
ローレンツ祭(2023年度)の資料
凝縮系物理とは
凝縮系物理の研究対象は、粒子の量子性が顕著な低温における物質の性質です。スピンを持つ電子の間に働く電磁相互作用と純粋な量子効果であるフェルミ統計性などが組合わさることで、凝縮系物質は金属や絶縁体、磁石や超伝導体といった様々な表情を見せてくれます。1980年代に発見された量子ホール効果と高温超伝導(どちらも、その発見に対してもノーベル賞が授与されています)は、その量子性の顕著な発現であり、その後の凝縮系物理の発展に多大な影響を与えてきました。
21世紀になり、凝縮系物理の研究対象はさらに大きな広がりを見せています。量子ホール効果の物理で強調された波動関数の量子力学的位相の効果は、位相幾何学的(トポロジカル)に特徴付けられた量子状態を示す「トポロジカル物質」へ引き継がれています。その代表的な例は、絶縁体でありながら表面のみが特異で強固な金属となるトポロジカル絶縁体と呼ばれる物質群です。その表面では、ディラック粒子と同じ線形なエネルギーと運動量の関係(分散関係)が電子の運動を支配しており、一昨年ノーベル賞を受けたグラフェンと呼ばれる物質と類似の特徴があります。一方、高温超伝導の研究の流れの中では、2008年にこれまで超伝導とは無縁であると考えられていた鉄を含む物質で高温超伝導が発見され、ホットな話題となっています。さらに、遷移金属化合物の研究が高温超伝導を引き金として新たな段階を迎えています。例えば、三角形の形状の結晶格子を持つ遷移金属化合物では、隣同士の相互作用の結果、格子点上のスピンの向きが決まらない困った状態が生じます(フラストレーション)。スピン(時には電荷)がフラストレートした状態がいろいろな物質で実現しており、フラストレーション系と呼ばれる研究分野が発展しています。 それらに加えて、数十から数ナノケルビン程度まで冷却された希薄原子・分子気 体系も21世紀の凝縮系物理の中心的な研究対象となっています。冷却気体系は光 格子(レーザーによって作られる周期ポテンシャル)に閉じ込めることで、構成 粒子同士が強く相互作用するいわゆる強相関領域を実現できます。この光格子中 冷却気体系では、密度、相互作用の強さ、格子の形状、構成粒子の種類、不純物 ポテンシャルなどの多岐にわたる性質が精密に制御でき、この長所を生かして数 多くの新しい量子多体現象が見いだされています。
これらの凝縮系物理の発展の重要なキーワードは「強相関効果」です。その典型は、強い電子間クーロン相互作用により電子の運動が著しく抑制され、絶縁体状態となるモット絶縁体です。このモット絶縁体は低次元構造を持つ磁性体やフラストレーションをもつ量子磁性体の舞台となります。モット絶縁体の中にキャリアを導入すると系は金属化します。しかし、もともとの強相関効果のため、通常の金属とは異なる特異な量子現象を示すことになります。銅酸化物で見られる高温超伝導はまさにこの特異性の表れといえます。
基礎物理学研究所の「物性基礎論:凝縮系物理グループ」では、この「強相関効果」をキーワードとして、高温超伝導に代表される強相関電子系の量子輸送現象や励起ダイナミクス、低次元磁性体やフラストレーションを持つ系の量子現象、冷却気体系の低次元超流動性と量子相転移と量子非平衡ダイナミクスなど、場の理論や大規模数値計算等の手法を駆使して研究を行っています。
一次元量子系の励起ダイナミクス
密度行列繰り込み群法は数値繰り込み群法の一種であり、低次元量子スピン系・電子系の研究に威力を発揮しています。この手法を動的性質(振動数に依存した物理量)の数値計算法として発展させ、世界第一位の性能を持つ神戸の「京」スーパーコンピュータ上で高性能なパフォーマンスを発揮できるようプログラムのチューニングと手法開発を行っています。そして、この動的密度行列繰り込み群法を用いた大規模数値計算により、一次元電子系・スピン系のスピンや電荷励起ダイナミクス、非平衡緩和ダイナミクスの解明を目指しています。これまでに、次世代非線形光学素子としての可能性を秘めている一次元モット絶縁体や、スピンと格子が結合してスピン励起にギャップが開くCuGeO3を念頭に置いた計算を行っています。
SPring-8 やJ-PARC 等の大規模量子ビーム施設の稼働やレーザー分光技術の進展により、量子スピン系・強相関電子系の励起ダイナミクスや非平衡ダイナミクスの研究が飛躍的に発展しています。そこから磁気応答・電荷応答・光学応答に特有の量子現象が出現する可能性があります。最先端の量子ビームを利用した研究とタイアップしながら、最新のスーパーコンピュータを用いた新しい量子現象の研究を進めています。
高温超伝導 -鉄系超伝導体の反強磁性相-
鉄系高温超伝導体の母物質は反強磁性金属相です。反強磁性秩序出現にはフェルミ面の形状とともに鉄イオン内の電子間相互作用が重要であると考えられています。銅酸化物ほど強くはありませんが、無視できるほど小さくもありません。また、電子状態の詳細を議論するには鉄の5 個の3d軌道を取り扱う必要があります。したがって、反強磁性金属相の物理は「多軌道相関系 の物理ということになります。
私たちは、5 軌道ハバード模型の反強磁性の基底状態を平均場近似で求めて、図1のようなバンド分散構造を決定しました。そして、そのバンド構造のもとでの動的スピン感受率を計算しました。その結果は非弾性中性子散乱の実験と非常によく対応していますが、そこで重要なのが電子-ホール連続帯励起と呼ばれるバンド構造を反映した励起です。光学伝導度も電子-ホール連続帯励起とそれを構成する軌道自由度に注目すると理解できます。最近、電荷励起を観測すると考えられていた共鳴非弾性X 線散乱によって、銅酸化物のマグノン励起が観測され注目を集めています。この手法を鉄系に適用し、スピンと電荷励起を同時に観測しようという試みが始まっています。その実験に先立ち、どのようなスピン・電荷・軌道分散やそれらの複合分散が得られるべきか理論から予測することは意味があるでしょう。そこで、共鳴非弾性X 線散乱スペクトルを計算して、マグノン励起のほかに、スピン・軌道複合励起の存在を予言しました。もしこの励起が実験で同定されれば、鉄砒素系超伝導体の軌道の効果が解明されることにつながるでしょう。
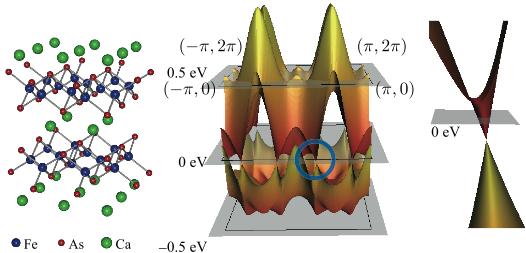
図1 鉄系高温超伝導体の結晶構造(左図)と母物質の反強磁性金属相におけるバンド分散構造(中図)。○印の領域にディラック型分散(右図)が存在する。
フラストレーション系とスピン液体
モット絶縁体の低温、低エネルギーの物理は、スピンで表された「有効ハミルトニアン」で記述されます。もちろん、「スピン」は量子的な実体なので、多数のスピンが相互作用する問題を解くのは一般に困難な問題であり、何らかの近似的な方法で理解するのが普通です。結晶格子が立方格子のように単純な構造を持っている時には、スピンの「量子性」(非可換性と言ってもよいでしょう)を一旦忘れて(古典極限)、局所的なエネルギーを最低にするような状態を見つけることで、実際の量子論的な基底状態の良い近似が得られることがわかっています。しかし、例えば三角形や四面体が頂点を共有しながらつながってできる結晶格子(「六つ目編み」と呼ばれる日本の竹カゴのパターンなどが典型例です)のようなものを考えると、局所的なエネルギーを最小化する状態が無数に出てきてこのような方法では駄目なことがわかります。このようなちょっと「病的な」状況が起こる系を「フラストレーション系」と呼びますが、このような系の特徴としてエネルギー最小の状態が簡単に決まらないことから、交換相互作用の強さに代表される磁気的なエネルギースケールよりも十分に低温に至るまで磁気秩序が発生しなかったり(図2の赤い領域)、通常は秩序を破壊する因子と思われている「熱ゆらぎ」、「量子ゆらぎ」で逆に特定の磁気秩序が選択される現象(order-by-disorder)が起こったりします。
この種の系に見られる巨視的縮退は、さまざまな「創発的な」現象の格好の舞台を提供します。 最近では、巨視的に縮退した最低エネルギー状態から、この種の系にある種のゲージ理論やモノポールに対応する励起が創発されることがあることもわかってきましたが、そのような面白い現象のひとつに「スピン液体」と呼ばれるちょっと変わった物質状態の出現があります。スピン液体にもいろいろな種類があるのですが、何の秩序もなく一見、常磁性状態と同じように見えるのに、系のトポロジーなどに関係した「隠れた」秩序があるのがミソです。最近、「トポロジカル物質相」が関心を集めていますが、スピン液体はそのひとつの例にもなっています。理論的にもきちんとその存在を示すのはそう簡単ではないのですが、これを実現する物質を探すのは長らく、量子磁性における「聖杯」と言われるぐらい困難でした。しかし、最近、カゴメ格子と呼ばれる「六つ目編み」パターンの結晶構造を持つ鉱物や、二次元性の強い有機化合物で有望な候補が見つかり関心が集まっています。
最近、私たちは、強い外部磁場をかけた磁性体の物性におけるスピンの量子性の効果を場の理論的な方法で調べ、強磁場下でも、量子力学的位相(スピンBerry位相)のためにいろいろな新しいタイプのスピン液体が起こり得ることを見いだしました。このようなスピン液体の強磁場下での物性を、微視的模型を用いて解析的・数値的に調べる研究が進行中です。また、この種の系の持つ「トポロジカル秩序」とエンタングルメントなどのような量子情報的な概念との関連にも関心を持っています。
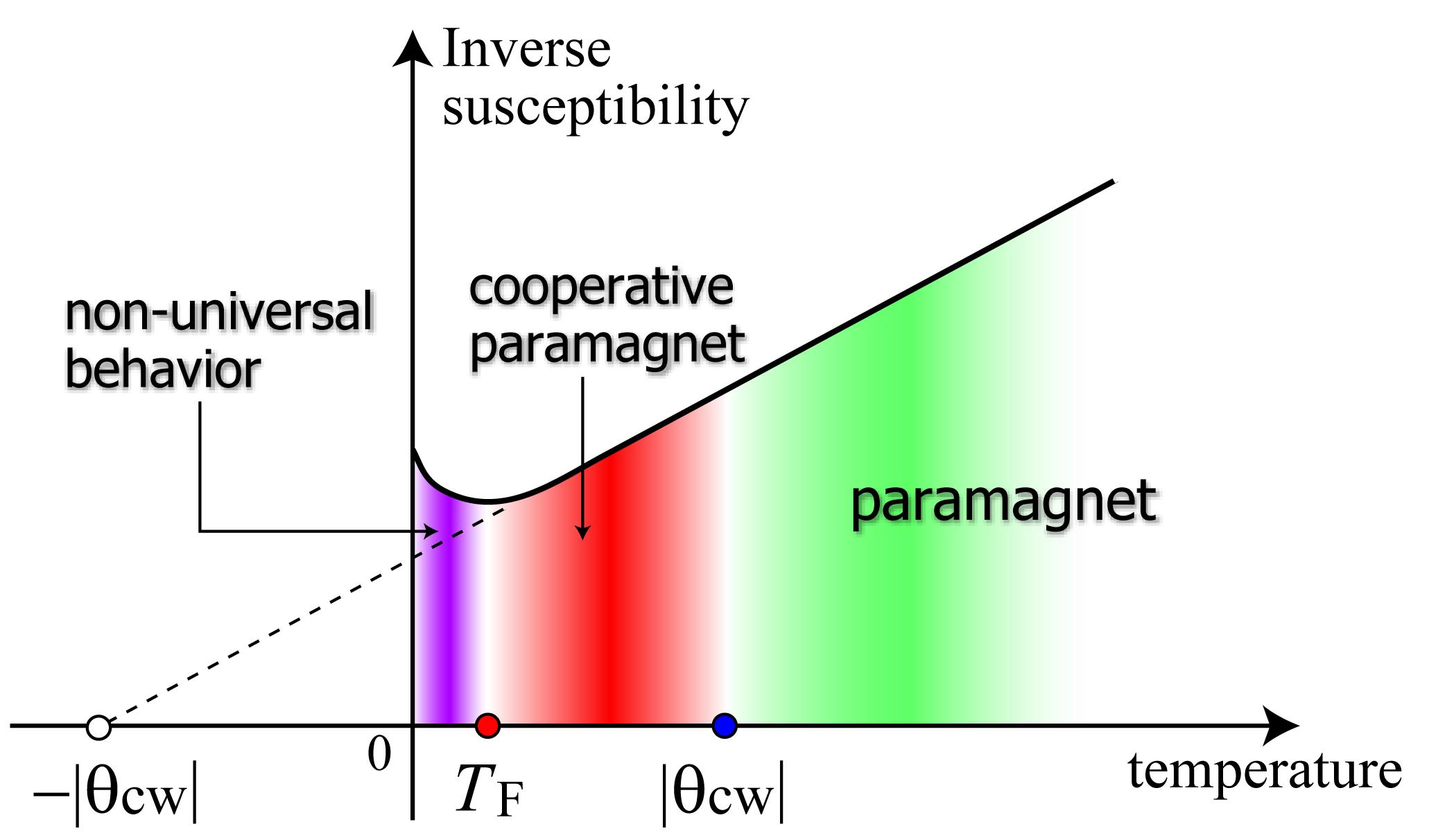
図2 フラストレーション系の温度による振る舞いの違い。典型的な磁気的エネルギースケールθCWより低温でも秩序化しない。
光格子中の一次元超流動
超流動状態にあるボース流体を非常に細長い空間に閉じ込めると、超流動性に どのような影響が出るでしょうか? 有名なHohenberg-Mermin-Wagnerの定理に よれば、完全に一次元的なボース流体は強い量子的及び熱的揺らぎのために有限 温度において超流動体たりえないことが知られています。真に絶対零度の物質系 などありませんから、この定理から「一次元では超流動現象は見られない」と結 論付けられるように思われます。しかしながら、実際に実験をやってみると事は そう単純ではないのです。
冷却気体系の実験では、強力な光格子を二方向(例えばyとz方向)から印加し てその二方向の運動を完全に禁制することで、一次元気体を作ることができます。 近年の実験では、さらに軸方向(x方向)にも比較的弱い光格子を加えて、周期ポ テンシャル中の一次元ボース気体の輸送特性が調べられています。その結果、上 で述べた予想に反して、一次元系でも散逸のない超流動流が観測されました。一 方で、超流動体においては一般に超流動流速を増大させていくと流れが超流動的 なものから散逸的なものに切り替わることが知られているのですが(切り替わる 流速をよく超流動臨界速度といいます)、一次元系においてはこの切り替わりが 高次元系に比べてずっと小さい流速で起こってしまいます。また、高次元系では この切り替わりはある速度を越えた際に急激に起こるのですが、一次元系の場合 はどこが閾値だか分からないくらいだらだらと起こります。このように、「一次 元系においても超流動現象は見られるが我々がよく知っている高次元のものとは ずいぶん違う」というのが実験から得られた知見です。
私たちは、この一次元超流動現象を時間発展塊毎間引き法という数値厳密手法、 朝永-Luttinger流体理論とインスタントン法という解析計算手法を用いて調べま した。その結果、量子揺らぎが引き起こす「位相滑り」という過程が一次元超流 動に特有の性質を与える主因となっているという結論に至りました。ここでいう 量子位相滑りとは、量子トンネルを介して超流動速度が減衰していくという現象 (図3)で、通常ミクロなスケールでしか起こらない量子トンネルが超流動 速度というマクロな量で起こるという意味で非常に珍しいものです。
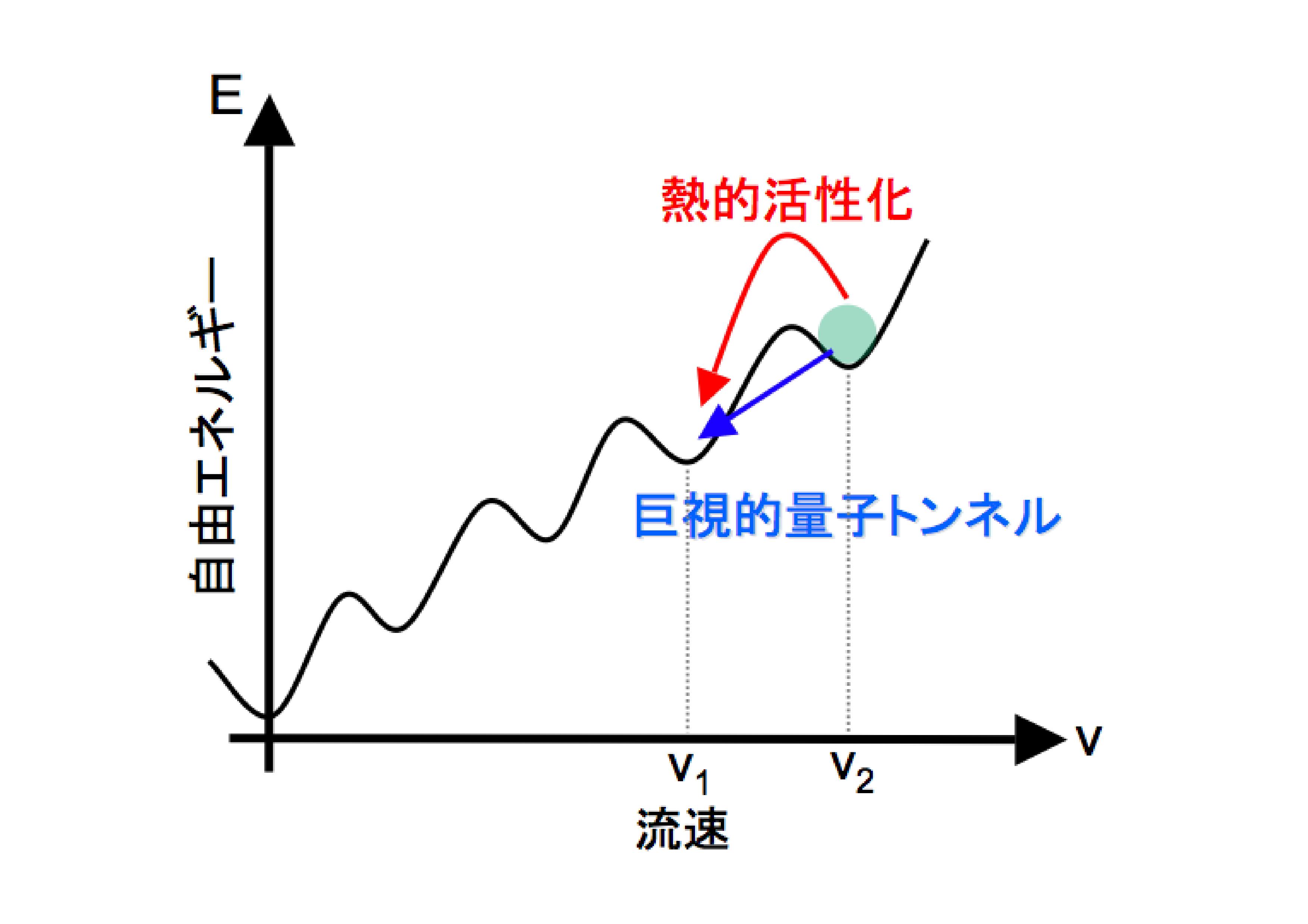
図3 位相滑りの概念図。青字で示されている方が量子位相滑り。