角運動量の保存

角運動量とは聞き慣れない言葉かもしれない。しかしフィギアスケートでスピン をする場合に両手を広げてゆっくりと回転する人が手を胸にあてると回転のスピー ドが速くなるのにも角運動量の保存則が使われている。

まず高校で習ったニュートンの運動方程式

 

m a= F (1)

を思い出そう。ここでm,a,Fはそれぞれ質点の質量、加速度、力である。 高校では1次元運動が主だった対象だったのでスカラーの式を書いていたが、 実際には力や加速度は方向を持ったベクトル量である。 従って

$$m \vec a=\vec F, \quad \vec a=\frac{d \vec v}{dt}$$ (2)

と書き直しておく方が良い。また加 速度$\vec a$,速度$\vec v$、位置$\vec x$はそれぞれ

$$\frac{d\vec v}{dt}=\vec a, \quad \frac{d\vec x}{dt}=\vec v$$ (3)

という関係で結ばれている事を思い出そう。(高校時代はスカラーの関係式しか 習っていないが、デカルト座標系では 各成分で独立の関係があるのでベクトルへの適用は問題ない)。 xy平面内の運動方程式を考えると(2)式から平面運動の運動方程式は

$$m\frac{d v_x}{dt}=F_x, \quad m \frac{d v_y}{dt}=F_y$$ (4)

である。ここで添字はx,y成分であることを示す。つまり $\vec x=(x,y),\vec v=(v_x,v_y),\vec F=(F_x,F_y)$等である。

さて(4)の第2式にxをかけ、第1式にyをかけて差を作ってみよう。

$$x\frac{dv_y}{dt}-y\frac{dv_x}{dt}=\frac{d}{dt}(xv_y-yv_x)$$ (5)

に注意すると

$$\frac{d}{dt}\{m(xv_y-yv_x)\}=xF_y-yF_x$$ (6)

が得られる。

(6)式の両辺に現われた量の意味は極座標を使うとはっきりする。 極座標で

$$x=r\cos\phi,\quad y=r\sin\phi$$ (7)

と書く。また速度とx軸のなす角を$\theta$とすると

$$v_x=v \cos\theta,\quad v_y=v\sin\theta$$ (8)

であるから

$$x v_y-y v_x=rv(\cos\phi\sin\theta-\sin\phi\cos\theta)=rv \sin(\theta-\phi)$$ (9)

となる。ここで原点から質点の位置を通るベクトル$\vec v$におろした垂線の長 さをr_pとすると $r_p=r\sin(\theta-\phi)$であり、従って

 

xv_y-yv_x=r_p v (10)

と書ける。r_pが一定とすると(6)の左辺は円周長と接線方向の速さに比例するという事に なる。

 

Figure 1: 循環流の例

以上の説明に対して 極座標を使う事への抵抗も同時にありそうである。ここでは図を用いて その意味を説明してみる。まず原点Oから中心力を受けて回転運動をする 粒子を考えてみよう(図1(a))。ここで粒子は点A,B,C,Dではそれぞれ矢印の向き に運動する。但し粒子の速度ベクトルの端点を粒子の位置から 始めるのではなく少しだけずらして描いてある。このとき例えばAにある場合 には中心力はx成分しか働かず、速度はy成分しか持たない。従ってこの場合 には(6)式は

$$m \frac{d (x(A)v_y(A)) }{dt}=x(A)F_y(A)$$ (11)

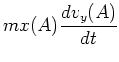となる。但し括弧(A)は点Aでの値を示す。こう書くと高校の物理を受けた事の ある者にもう少し意味がはっきりするであろう。右辺は力のモーメント(トルク) である。一方、左辺ではA点にいる瞬間にはx(A)は時間変化がない、即ちx方向に速度がないので左辺を $m x(A)\displaystyle\frac{dv_y(A)}{dt}$と書き変えら れる。従って、左辺の意味は運動量に回転半径をかけたものになっている。この ことは他の点B,C,Dでも同様に成り立つ。この左辺を角運動量の微分と呼んでい る。

一方、もっと一般に図1(b)のような循環を考えてみよう。この場合はx,y軸に 対して斜めの流れもある。上で考えた様な簡単な考察は破綻するように思うが、 実は問題はない。というのはそもそも(2)式はベクトルの式 であるし、ベクトルは 図2にあるように好きな方向に分解できるからである。一般論を簡単に議論しようと するなら最初からベクトル形式で議論した方が良いであろうことは想像がつく。 実際、物理学基礎論Aではそういった説明がなされるであろう。しかし諸君の場 合は運動方程式はベクトルであって、それを使った方が便利であるという事だけ を心に留めておけば充分である。

 

Figure 2: ベクトルの分解

このようにして(11)式が角運動量の変化がトルクによって生じるという事 を示している事を理解できたであろう。従ってトルクがなければ角運動量は保存 する。 またこの式の3次元化も容易である。と いうのは今、xy平面で考えた事を、それぞれyz,zx平面で考えれば良い。こ こでもベクトルは合成、分解可能であることを利用すると、一般の3次元ベクト ルをそれぞれ3つの平面に射影して平面問題として議論し、それを足し合わせれ ば3次元の場合の角運動量の保存則となる。