

Next: 応用例:浅い水の波
Up: No Title
Previous: No Title
一般の流体では流体の流速が一様でないときに、内部摩擦によって
境界面にずり(せん断)による抵抗力が働き相対速度を減らそうとする。
この性質を粘性という。流体の入っている容器を回転させると流体も次第に
回転し始めて、また容器を静止させると流体も次第に速度を失うのは粘性の
影響である。
しかし、その一方で空気の様に極めて粘性の低い流体もある。
そこで割り切って粘性を完全に無視すると著しく取扱が簡単になり、かつ様々な
現象を説明することが可能になった。こういった流体を完全流体と呼ぶ。
ベルヌーイの定理の本質はエネルギーの保存である。粘性を考慮すると
エネルギーが保存しないので、
対象は完全流体、すなわち粘性の入っていない流体である。
まず重力下の質点(質量m)のエネルギーの保存を思い出そう。質点の速さをvとすると
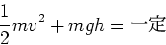 |
(1) |
ここでgは重力加速度、hは質点の位置(高さ)である。
この式はジェットコースターを思い出せば納得
するのではないか。即ち高い処に上がって一挙に降りるとスピードが出る事の根
拠である。
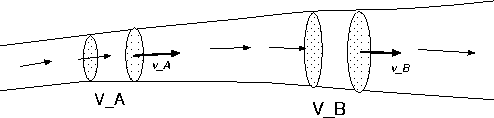
Figure 1:
斜線がかかったところが流管の断面。体積VA,VBは断面に囲まれ
た領域。矢印は流れを表す。速さはそれぞれvA,vB
 |
さて重力下の縮まない流体の運動を考えてみよう。その場合、
流体の(質量)密度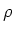 は常にどこでも一定
である。
流れに沿って管を考える。
領域Aでの体積をVA,領域Bでの体積をVBとすると、それぞれの部分の質量
は
は常にどこでも一定
である。
流れに沿って管を考える。
領域Aでの体積をVA,領域Bでの体積をVBとすると、それぞれの部分の質量
は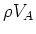 ,
,
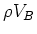 となる。
定常流では領域Aにあった流体が全て領域Bに移ると考えられ、
その質量は保存するために
となる。
定常流では領域Aにあった流体が全て領域Bに移ると考えられ、
その質量は保存するために
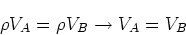 |
(2) |
が成り立つ。一方、流体がAからBまで流れると
| 運動エネルギー |
: |
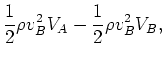 |
|
| 位置エネルギー |
: |
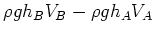 |
(3) |
だけ増加する。ここで添字をつけたvi,hi (i=A,B)はそれぞれ流体の速さ
と領域iの高さである。ここで質点の場合と異なるのは運動エネルギーと位置
エネルギーの和が保存しない点である。その差は流体には圧力があり、
上流の流体
に押し出された仕事 と、下流の流体を押し出した仕事の差は
であり、それが力学的エネルギーの増加分に等しい。但しPA,PBは領域A,Bでの流体の圧力である。(完全流体の場合は圧力の作用は運動方向に一致し、
側面には仕事はしない)。
以上の(2)-(4)を組み合わせる事で
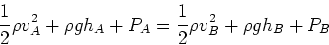 |
(5) |
となる。領域A,Bは任意に選んだために、流れに沿って
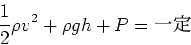 |
(6) |
が成立する。これがベルヌーイの定理である。
ベルヌーイの定理の導出で仮定された縮まない流体という仮定は外しても
定理は成立する。但しその場合は表式が(6)式と異なる。一方、実際の流
体の様に粘性を考慮すると最早定理そのものは成立しない。しかし空気等での高
速の流れ等では粘性の影響は小さく近似的に成り立っていると考えて差し支えな
い。
Hisao Hayakawa
2000-02-07