Permanent Exhibition
Permanent Exhibition
Solitons are very stable solitary waves in a solution of those equations. As the term "soliton" suggests, these solitary waves behave like "particles". When they are located mutually far apart, each of them is approximately a traveling wave with constant shape and velocity. As two such solitary waves get closer, they gradually deform and finally merge into a single wave packet; this wave packet, however, soon splits into two solitary waves with the same shape and velocity before "collision".
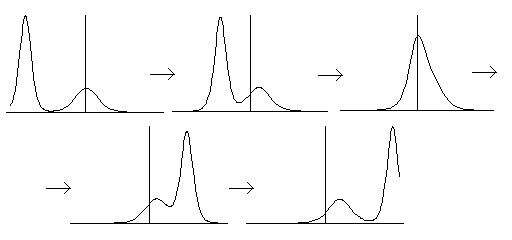
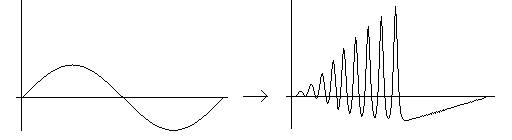
The stability of solitons stems from the delicate balance of "nonlinearity" and "dispersion" in the model equations. Nonlinearity drives a solitary wave to concentrate further; dispersion is the effect to spread such a localized wave. If one of these two competing effects is lost, solitons become unstable and, eventually, cease to exist. In this respect, solitons are completely different from "linear waves" like sinusoidal waves. In fact, sinusoidal waves are rather unstable in some model equations of soliton phenomena. Computer simulations show that they soon break into a train of solitons.
In this exhibition, we present several model equations of soliton phenomena along with soliton solutions. These equations are the most fundamental examples of the so called "integrable systems". Besides soliton solutions, these model equations exhibit many remarkable properties, which invoked a wide range of researches since the 1960's.
