Permanent Exhibition

Switch to Japanese

Next Room

KdV equation u_t + u_xxx + 6uu_x= 0

The Korteweg-de Vries (KdV) equation is the champion of model equations of nonlinear waves. It was studied by Korteweg and de Vries late in the 19th century as a water wave equation, and after a long period of sleep, revived as one of the most fundamental equation of soliton phenomena. In fact, it is from numerical experiments of this equation that Zabusky and Kruskal introduced the term "soliton".

• 2-soliton solution [gif]
  Here is an animation of the 2-soliton solution (solution with two solitons). Solitons emerge as peeks of the solution. A tall (fast) soliton is approaching a little (slow) soliton from the left. They will soon merge, and separate again. Be sure that the ratio of height and width is quite large; the real profile is more like a flatter water wave just like the soliton observed by Scott Russel.
  
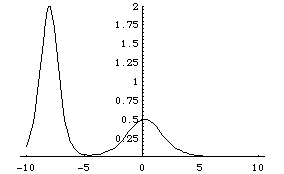
  [profile of 2-soliton solution before collision]
  solution: u = 2*(Log f)_{xx},
  f = 1 + Exp[eta1] + Exp[eta2] + c12*Exp[eta1+eta2],
  eta1 = k1*(x - x1) - k1^3*t, eta2 = k2*(x - x2) - k2^3*t,
  c12 = (k1-k2)^2 / (k1+k2)^2.
  parameters: k1 = 2, k2 = 1, x1 = -8, x2 = -2.
  

• Emergence of solitons from sinusoidal wave [gif]
  Zabusky and Kruskal discovered solitons in numerical solutions of the KdV equation. Here is an animation of such a numerical solution. The setting is almost the same as the computation of Zabusky and Kruskal: 1) The equation is solved by the same difference scheme (the Cranck - Nicolson or "leap-frog" method). 2) The equation is solved under a periodic boundary condition. 3) The initial value is a sinusoidal wave with one period over the whole space.

  The numerical solution shows that the sinusoidal wave soon developes into a train of solitons. The tail of the soliton train grows backward, and eventually overlap with the head solitons. You can observe collision of solitons in this overlapping region.
  
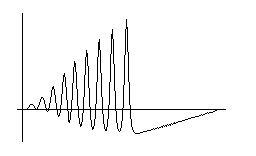
  [soliton train developed from sinusoidal initial value]