Permanent Exhibition

Switch to Japanese

Next Room

Modified KdV equation v_t + v_xxx + 6v²v_x= 0

The modified KdV equation differs from the original KdV equation in the last nonlinear term only. This, however, causes several substantial differences; the superficial similarity is rather inessential. On the other hand, these two equations are linked at a deeper level by the so called "Miura transformation".

• 2-soliton solution [gif]
  Here is an animation of the 2-soliton solution of the modified KdV equation. The profile and the process of collision are qualitatively very similar to the 2-soliton solution of the KdV equation. The analytical expression of the solutions, however, are completely different.
  
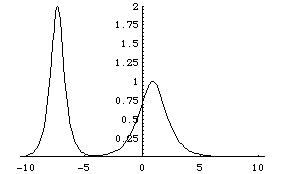
  [profile of 2-soliton solution before collision]
  solution: v = 2*(g_x * f - g * f_x)/(f^2 + g^2),
  f = 1 - c12*Exp[eta1+eta2]/(4*k1*k2),
  g = Exp[eta1]/(2*k1) + Exp[eta2]/(2*k2),
  eta1 = k1*(x - x1) - k1^3*t, eta2 = k2*(x - x2) - k2^3*t,
  c12 = (k1-k2)^2 / (k1+k2)^2.
  parameters: k1 = 2, k2 = 1, x1 = -8, x2 = -2.
  

• Emergence of solitons from sinusoidal wave [gif]
  Here is an animation of a numerical solution that imitates the computation of Zabusky and Kruskal. The initial value is a sinusoidal wave. The result is half similar to the KdV equation, but also considerably different. Unlike the case of the KdV equation, two trains of solitons emerge from the top and bottom of the sinusoidal wave.
  
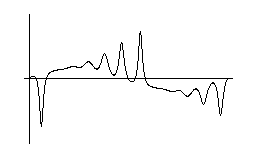
  [two soliton trains developed from sinusoidal initial value]