常設展示

Switch to English

次の部屋

変形 KdV 方程式v_t + v_xxx + 6v²v_x= 0

変形 KdV 方程式はもとの KdV 方程式と最後の非線形項が異なるだけである。 しかしこれがいくつかの実質的な相違を生む。見かけの相似性はむしろ 本質ではない。他方、これら２つの方程式はいわゆる「Miura 変換」に よってより深いレベルで結ばれている。

• 2-soliton solution [gif]
  ここにお見せするのは変形 KdV 方程式の２-ソリトン解の 動画である。波形と衝突過程は定性的には KdV 方程式の ２-ソリトン解とよく似ている。しかし解の解析的な表示は まったく異なる。
  
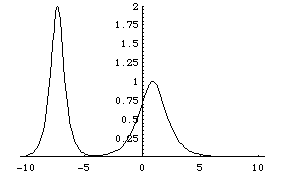
  [profile of 2-soliton solution before collision]
  solution: v = 2*(g_x * f - g * f_x)/(f^2 + g^2),
  f = 1 - c12*Exp[eta1+eta2]/(4*k1*k2),
  g = Exp[eta1]/(2*k1) + Exp[eta2]/(2*k2),
  eta1 = k1*(x - x1) - k1^3*t, eta2 = k2*(x - x2) - k2^3*t,
  c12 = (k1-k2)^2 / (k1+k2)^2.
  parameters: k1 = 2, k2 = 1, x1 = -8, x2 = -2.
  

• Emergence of solitons from sinusoidal wave [gif]
  ここにお見せするのは Zabusky と Kruskal の数値計算を 真似た数値解である。初期値は正弦波である。結果は 半ば KdV 方程式に似ているが、相当に異なる面もある。 KdV方程式の場合と違って、２つのソリトン列が正弦波の 頂上と底から出現している。
  
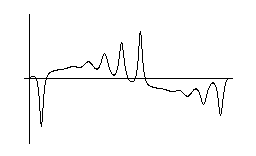
  [two soliton trains developed from sinusoidal initial value]