常設展示

Switch to English

展示室入口

Sine-Gordon 方程式 u_tt - u_xx + sin u = 0

「sine-Gordon 方程式」という言葉はおそらく一種の冗談で、 明らかに相対論的場の理論の「Klein-Gordon 方程式」から来ている。 この名が示すように、この方程式は1+1次元次空の相対論的非線形方程式 である。KdV 方程式同様、その先駆けは１９世紀の数学（Darboux の 曲面の幾何学の仕事）に見い出される。sine-Gordon 方程式もまた、 相対論的場の理論にとどまらず、固体物理、非線形光学、など広範囲の 応用をもっている。

解を可視化するため、ここでは連成振り子模型を用いる。 これは力学的な模型で、弾性のあるワイアー（あるいはむしろ、バネ） に等間隔で垂直に棒を刺したものからなる。棒は振り子として振舞い、 ワイアーのねじれを通じて隣合う棒から角方向の力を受ける。 （ワイアーと棒の代わりにゴムひもとマチ針を使えばもっと安価な 実験ができる。）棒の間隔が０になる極限で、この力学的模型は sine-Gordon 方程式に近づくのである。

sine-Gordon 方程式のソリトン解は KdV や変形 KdV 方程式よりも はるかに多様である。１-ソリトン解ですら、「キンク」と「反キンク」 の２つの異なる場合がある。キンクは左の無限遠方で０、右の無限遠方 で２πの境界値をとる解である。反キンクの境界値は０と-２πである。 もっと直観的に言えば、いずれの場合も振り子の列はワイアーに 沿って１回、ただし逆向きに、回る。同様に、２-ソリトン解は、 ２個のキンクの衝突、２個の反キンクの衝突、キンクと反キンク、 および「breather（呼吸）解」と呼ばれる一種の「束縛状態」とに 分類される。「呼吸」解を言葉で説明するのは難しいが、動画では その振舞いがはっきりわかる。

• kink-antikink collision [gif]
  ここお見せするのはキンク-反キンクの衝突の動画である。 キンクと反キンクは逆向きに同じ速さを与えられている。 振り子の列の捻れが衝突中のある瞬間（t = 0）に消えている ことに注目されたい。
  
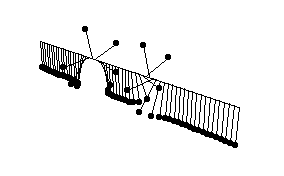
  [kink-antikink solution before collision (coupled pendulum model)]
  solution: u = 4*Arctan[ (p*Sinh[Sqrt[p^2 - 1]*t]) / (Sqrt[p^2 - 1]*Cosh[p*x]) ].
  parameters: p = 2.
  

• kink-kink collision [gif]
  ここでお見せするのはキンク-キンク衝突の動画である。 キンクは同じ向きに捻れているので、振り子は衝突の間も （２巻き）捻れたままである。面白いことに、２つの キンクは衝突するというよりはむしろ「反発」するように 見える。（この動画を作るまではこういう現象をまったく 想像していなかった！）
  
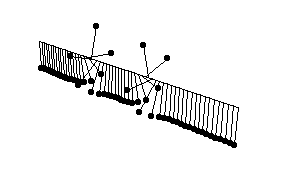
  [kink-kink solution before collision (coupled pendulum model)]
  solution: u = 4*Arctan[ (Sqrt[p^2 -1]*Sinh[p*x]) / (p*Cosh[Sqrt[p^2 - 1]*t]) ].
  parameters: p = 2.
  

• breather solution [gif]
  ここでお見せするのは「呼吸解」の動画である。 この名前は波形の振舞いに由来している。波形は 規則的に上下に振動するので、息をしているように 見えるのである。動画でわかるように、振り子模型 ではこの振舞いは局在した集団的振動に他ならない。
  
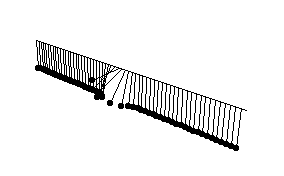
  [breather solution (coupled pendulum model)]
  solution: u = 4*Arctan[ (p*Sin[Sqrt[p^2 +1]*t]) / (Sqrt[p^2 + 1]*Cosh[p*x]) ].
  parameters: p = 2.