

 のマークは必須!)
のマークは必須!)
Kepler運動の方程式

を改良Euler法で解くプログラムを作りましょう。 平面上での運動を仮定し、初期条件は
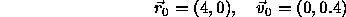
としてください。 また、時刻 t = 50 までを n = 2000 ステップに分割して解いて下さい。
 ケプラー問題をデカルト座標で解くプログラム (prog06.f)
ケプラー問題をデカルト座標で解くプログラム (prog06.f)
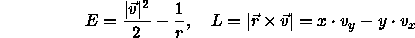
となります。 これらは保存量ですから(式の上で時間微分をとって 確かめましょう)、数値解がどの程度正しいかの目安になります。 力学の教えるところでは、E>0 のとき双曲線、E=0 のとき放物線、 E<0 のとき楕円の軌道を描きます。
 やり方はここ
やり方はここ
今週のプログラムには、FORTRAN の文法上、特に新しい所はありません。 これまでの知識を使って取り組んでみましょう。
この運動方程式を極座標表示を用いて解く プログラム も用意しました。解読できるでしょうか。
ap1: f90 ex061.f
ap1: a.out < ex061.in > ex061.dat
ap1: gnuplot ex061.plt

で n=-2 がKepler運動でした。 n=1 なら調和振動子です。 他の n では?
n=-1, xi=4.0, vyi=0.4 の場合の軌道
(t=200.0d0 まで計算した結果です。)
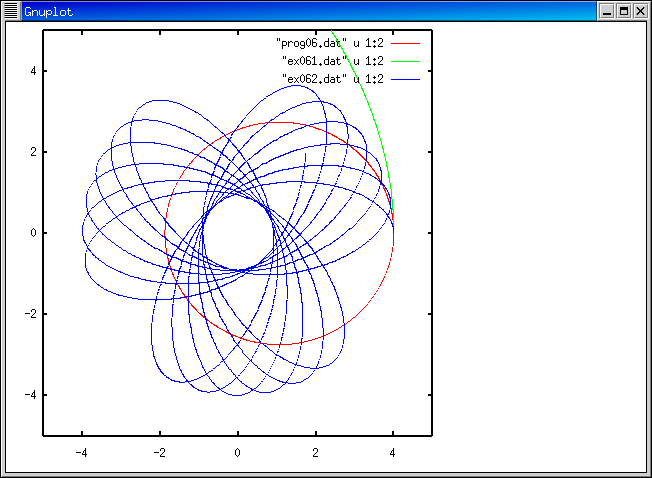
ap1: f90 ex062.f
ap1: a.out < ex062.in > ex062.dat
ap1: gnuplot ex062.plt
出席の返事の代わりに、プログラムを mule から直接送ってみて下さい。
 やりかたはここ
やりかたはここ