Table of Contents
概要
Siは半導体であることはよく知られています。 このSiを使って、エネルギーバンドを計算方法を習得し、PWscfの基本的な使い方を身に付けます。 また、対称点の指定を行うことで、バンド分散をどのように描くのかについても勉強します。 最後に、実空間における電荷密度の分布の計算も行います。
計算を実行するにあたり、事前に集めておく情報は、
- 結晶のブラべー格子の種類と格子定数
- 結晶の単位胞に含まれる原子の種類・数・原子量・位置
です。 原子の種類に応じて、擬ポテンシャルのデータを含んだファイルを別途用意する必要があります。
Si(ケイ素)について
単体のSiは最もよく知られている半導体で、その結晶構造はダイヤモンド構造です。 Siの化合物は岩石の成分として含まれているので、身の回りに最もありふれた元素の一つとも言えます。 現在のエレクトロニクスの成功は、 Si単体の結晶が高純度(99.999999999%)で作成できることもさるものながら、ハートリー・フォック近似を用いる第一原理計算によってその物性が計算できるところも大きいと考えられます。
以上のことから、Siは第一原理計算の入門の題材として適した素材であるといえます。
バンド計算
入力ファイルの作成
まず作業ディレクトリSiを作成し、そこで作業することにします。
$ mkdir Si $ cd Si
Quantum ESPRESSOは擬ポテンシャル法に基づく第一原理計算ソフトなので、電子状態の計算には擬ポテンシャルのデータ・ファイルが必要です。 擬ポテンシャルは、その作成の方法によっていくつかの種類が用意されていますが、今回はSi.pz-vbc.UPFをダウンロードします。
- 今回は単体なので擬ポテンシャルのファイルの種類はあまり問題になりませんが、複数の原子を使う化合物だと、いろいろな原子の擬ポテンシャルのファイルを組み合わせる必要が出てきます。
- その際に、WIEN2kのような全電子近似を用いた第一原理計算の結果を使って、本当に正しいバンドになっているかを確認します
- それならQuantumESPRESSOいらんやんけ…という話になりますが、バンド計算をしたあとの処理に関しては擬ポテンシャル法の方が高速に計算できるので向いています。
- バンド分散、状態密度、フェルミ面、電荷密度分布などの一粒子状態に基づく量を計算したい場合はWIEN2kの方が便利です。
- また、角度分解光電子分光やde Haas-van Alphen効果、Shubnikov-de Haas効果などの実験から推定されるバンド構造やフェルミ面の情報を元に、最適な擬ポテンシャルの組み合わせを探すこともあります。
ディレクトリSiの中に次のファイルを作成します(scfはself-consistent fieldの略)。
- Si.scf.in
&control prefix = 'Si', calculation = 'scf', pseudo_dir = './pseudo/', outdir = './tmp/', / &system ibrav = 2, celldm(1) = 10.26, nat = 2, ntyp = 1, ecutwfc = 12.0, / &electrons conv_thr = 1.0d-8 / ATOMIC_SPECIES Si 28.086 Si.pz-vbc.UPF ATOMIC_POSITIONS Si 0.00 0.00 0.00 Si 0.25 0.25 0.25 K_POINTS automatic 6 6 6 1 1 1
入力ファイルの各パラメータは、Quantum ESPRESSOのインストール・ディレクトリの中にある PW/Doc/INPUT PW.html というファイルを参照すれば書いてあります。 もしパラメータを指定しなければ、デフォルトの値が使われます。 今回は入門編ということで、最低限、指定しなければいけないもののみ指定します。 指定する順番は任意です。
&control
計算データの入出力に関する情報を指定します。
| 変数 | 初期値 | 説明 |
|---|---|---|
| prefix | pwscf | 得られた計算の結果のデータの保存名 |
| calculation | scf | 計算の種類。scfは固有状態計算。 |
| pseudo_dir | $HOME/espresso/pseudo/ | 擬ポテンシャルファイルの保存場所 |
| outdir | ./ | 計算の結果の保存場所。指定しなければ計算を実行したディレクトリになる |
&system
結晶構造に関する情報を指定します。 以下のパラメータはすべて初期値が設定されていませんので、ユーザーが必ず入力する必要があります。
| 変数 | 初期値 | 説明 |
|---|---|---|
| ibrav | なし | 結晶がどのブラベー格子に属するかを指定。2は面心立方格子である。 |
| celldm(1) | なし | ボーア半径を1としたときのブラベー格子の格子定数a。オングストロームで指定したければ代わりに変数Aを使います |
| nat | なし | 単位胞に含まれる原子の総数。Siはダイヤモンド構造をとるので2です。 |
| ntype | なし | 原子の種類の数。今の場合は単体のSiなので1です。 |
| ecutwfc | なし | リュードベリ・エネルギー単位とする波動関数の運動エネルギーのカットオフ。大きくするほど計算の精度は上がるが計算時間が長くなる。 |
&electrons
実際の計算にあたってのオプションです。
| 変数 | 初期値 | 説明 |
|---|---|---|
| conv_thr | 1.0d-6 | SCF計算におけるエネルギーの収束判定。デフォルトだとややゆるいので厳しめにします。 |
ATOMIC_SPECIES
使用する原子の種類、原子量、擬ポテンシャルのファイル名を指定します。
ATOMIC_POSITIONS
alat (celldim(1)あるいはAのこと)を1としたときの原子の単位胞内における位置をデカルト座標で指定します。
K_POINTS
計算に使うk点を指定します。
- automaticオプションにより自動的に逆格子を6×6×6に分割したものを使います (Monkhorst-Pack grid)。分割の数が多ければ多きほど計算が正確になりますが、それだけ計算に時間がかかるようになります。
- 後ろの3つの数字は、分割した点のk点を使うなら0、分割した点と点の中間点を使うなら1を指定します(つまり0を指定したらガンマ点が含まれますが、1を指定すると含まれません)。
- 半分だけずらした方が、少ないk点数でより精度が高くなることが知られています
計算の実行
端末からpw.xを実行します。
$ pw.x < Si.scf.in > Si.scf.out
実行したら、計算の途中経過が出力された Si.scf.out というファイルと、電荷密度などの計算結果のファイルが入った tmp/Si.save/ というディレクトリができます。 計算に失敗したら crash という名前のファイルもできるので、それを開いて原因を確認します。 計算が収束する様子は Si.scf.out の estimated scf accuracy を見ることで確認できます。
$ grep -e 'estimated scf' Si.scf.out estimated scf accuracy < 0.04383890 Ry estimated scf accuracy < 0.00208552 Ry estimated scf accuracy < 0.00003904 Ry estimated scf accuracy < 0.00000224 Ry estimated scf accuracy < 0.00000008 Ry
Siは半導体ですので Si.scf.out にフェルミ準位が表示されません。 その代わりに、価電子帯のトップのエネルギーが表示されます。 あとのバンド計算で必要ですので確認しておきます。
$ grep -e 'highest' Si.scf.out highest occupied level (ev): 4.4741
特定のk点におけるエネルギー
以下の手順で入力ファイルを作成します。
- Si.scf.in をコピーして Si.bands.in というファイル名にします。
- &control の calculation を scf から bands にします。
- &systemにnbnd=8という記述を加えます。nbndは計算するバンドの数です。
- Siの電子配置は[Ne]3s23p2なので、価電子は4つあります。
- 単位胞に2つのSi原子が含まれるので、価電子帯のバンドの数は8本になります。
- ただし、非磁性の場合の計算はエネルギーはスピンについて縮退しているので、バンドの数は結局4本になります。
- nbndは指定しなければ自動的に価電子帯のバンドの数(今の場合は4)になります。
- バンド計算の際は、伝導帯のバンドも見えないと不便なので、多めにバンドの数をとってやるわけです。
- 今回は、3sと3pのすべてのバンドが見えるように8としました。
- K_POINTS にエネルギーを計算するk点を指定します。
最終的にファイルは次のようになります。
- Si.bands.in
&control prefix = 'Si', calculation = 'bands', pseudo_dir = './pseudo/', outdir = './tmp/', / &system ibrav = 2, celldm(1) = 10.26, nat = 2, ntyp = 1, ecutwfc = 12.0, nbnd = 8 / &electrons conv_thr = 1.0d-8 / ATOMIC_SPECIES Si 28.086 Si.pbe-rrkj.UPF ATOMIC_POSITIONS Si 0.00 0.00 0.00 Si 0.25 0.25 0.25 K_POINTS 3 0.0 0.0 0.0 1 1.0 0.0 0.0 2 0.5 0.5 0.5 3
K_POINTSの下にある数字の3は、3つのk点でエネルギーを計算することを指定します。 その下に各k点の座標と、1から3の番号付けを書きます。 座標はデカルト座標で、2π/aを単位とします。
再び端末からPWscfを実行します。
$ pw.x < Si.bands.in > Si.bands.out
プログラムの実行により作成された Si.bands.out から指定したk点におけるエネルギーがわかります。
- Si.bands.out
(中略) k = 0.0000 0.0000 0.0000 ( 229 PWs) bands (ev): -6.3225 4.5875 4.5875 4.5875 6.3731 7.0827 7.0827 7.0827 k = 1.0000 0.0000 0.0000 ( 222 PWs) bands (ev): -2.6903 -2.6903 2.0923 2.0923 5.5112 5.5112 13.3516 13.3516 k = 0.5000 0.5000 0.5000 ( 228 PWs) bands (ev): -4.3138 -1.7254 3.5130 3.5130 5.5922 7.9810 7.9810 11.8807 (中略)
バンド構造のプロット
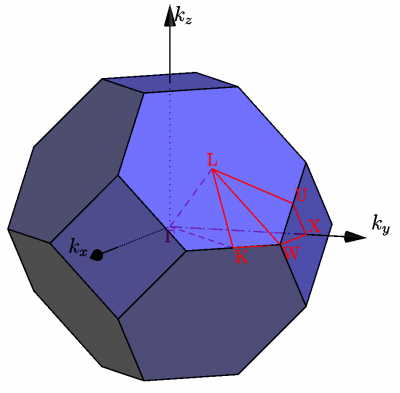
計算がうまく実行できることがわかったら、今度は逆格子空間で対称点を結んだ線上のバンド構造を計算しましょう。 Quantum ESPRESSOにはバンド構造を描くプログラムが含まれているので、それを利用します。
Si.bands.inを開いて、バンドを描く経路を指定します。 例としてK_POINTSで
- L点2π/a(1/2, 1/2, 1/2) → Γ点2π/a(0, 0, 0) → X点2π/a(0, 0, 1) → K点2π/a(0, 1, 1) → Γ点
という経路のk点の座標を入力します。 ここでaは格子定数です。
- Si.bands.in
&control prefix = 'Si', calculation = 'bands', pseudo_dir = './pseudo/', outdir = './tmp/', / &system ibrav = 2, celldm(1) = 10.26, nat = 2, ntyp = 1, ecutwfc = 12.0, nbnd = 8 / &electrons conv_thr = 1.0d-8 / ATOMIC_SPECIES Si 28.086 Si.pbe-rrkj.UPF ATOMIC_POSITIONS Si 0.00 0.00 0.00 Si 0.25 0.25 0.25 K_POINTS tpiba_b 5 0.5 0.5 0.5 5 0.0 0.0 0.0 10 0.0 0.0 1.0 10 0.0 1.0 1.0 10 0.0 0.0 0.0 0
- tpiba_bはバンドをプロットするためのk点を自動生成するオプションです。
- 2π/aを単位としたデカルト座標で指定します。
- 各行の4つ目の数字は、次のk点までの間に何個点を取るかを指定します(最終行の4つ目の数字は無視されます)。
作成できたら、PWscfを使ってエネルギー分散を計算します。
$ pw.x < Si.bands.in > Si.bands.out
次に、バンド構造をプロットするために必要なファイルを作成します。
- bands.in
&bands prefix = 'Si', outdir = './tmp/', filband = 'bands.dat', /
prefix や outdir はさきほど指定したものと同じものにします。 これを bands.x というプログラムで実行します。
$ bands.x < bands.in > bands.out
bands.outとbands.datが生成されたら成功です。 これらのファイルを開いて中身にエラーが出ているようなら、入力ファイルに間違いがないか確認してやり直しましょう。
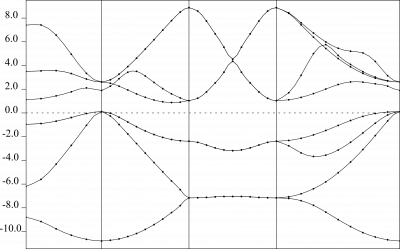
さて、以上で得られたデータを元に、バンド分散をplotband.xというプログラムを使って描いてみます。
指示に従って入力します。
$ plotband.x
Input file > bands.dat
Reading 8 bands at 36 k-points
Range: -5.6940 16.4680eV Emin, Emax > -7.0 14.0
high-symmetry point: 0.5000 0.5000 0.5000 x coordinate 0.0000
high-symmetry point: 0.0000 0.0000 0.0000 x coordinate 0.8660
high-symmetry point: 0.0000 0.0000 1.0000 x coordinate 1.8660
high-symmetry point: 0.0000 1.0000 1.0000 x coordinate 2.8660
high-symmetry point: 0.0000 0.0000 0.0000 x coordinate 4.2802
output file (xmgr) > Si.bands.xmgr
bands in xmgr format written to file si.bands.xmgr
output file (ps) > Si.bands.ps
Efermi > 4.4741
deltaE, reference E (for tics) 1.0 4.4741
bands in PostScript? format written to file si.bands.ps
- Range … どこまでのエネルギーの範囲をプロットするか、エネルギーの最高値と最低値の表示を参考に決めます。
- output file (xmgr) … Graceというグラフ描画ソフト用の出力ファイルの名前を指定します。 また、output file (ps)は、Postscript用のファイルです。
- Efermi … フェルミ・エネルギーを指定しますが、今の場合は半導体なので、さっき調べた価電子帯のトップのエネルギーを入力します。
- deltaE … グラフのエネルギーの刻み幅
- reference E … 刻みの基準となるエネルギーの値
XCrysDenによるバンドの経路の指定
実は、バンドの経路はXCrysDenを使って指定すると非常に楽です。
- XCrysDenを起動し、[File]→ [Open PEscf …] → [Open PWscf Input File] から Si.scf.in を開きます。
- [Tools] → [k-path Selection]を選ぶことで、ブリルアンゾーンから経路を選ぶことができます。
- 選び終えたら[OK]を押し、“Total number of k-points along the path”でk点数を指定した後、“File of type”でpwscfを選んで適当な名前をつけて保存します。
- 得られたk点の経路を Si.bands.in の K_POINTS に貼り付けます。
電荷密度分布の計算
ミラー面[1, −1, 0]で結晶を切り、そこでの電荷の分布を調べます。
電荷密度の計算には pp.x というプログラムを使用します。 まず、以下のようなファイルを作成します。
- Si.pp_rho.in
&inputpp prefix = 'silicon', outdir = './tmp/', filplot = 'sicharge', plot_num= 0, / &plot nfile = 1 filepp(1) = 'sicharge' weight(1) = 1.0 iflag = 2 output_format = 2 fileout = 'Si.rho.dat' e1(1) = 1.0, e1(2) = 1.0, e1(3) = 0.0, e2(1) = 0.0, e2(2) = 0.0, e2(3) = 1.0, nx=56, ny=40 /
pp.xはまず&inputppを読み込んでプログラムを実行して必要な情報を計算した後、&plotを読み込んでグラフにプロットできる形式にします。 どちらか片方の計算を行いたい場合は、そのブロックのみを残して他は消してください。
&inputpp
入力ファイルと出力ファイルの設定を行います。
| 変数 | 初期値 | 説明 |
|---|---|---|
| filplot | なし | 計算結果の出力ファイル |
| plot_num | なし | 計算する物理量を指定。0は電荷密度を表す。 |
&plot
電荷密度をプロットするのに必要な部分です。
| 変数 | 初期値 | 説明 |
|---|---|---|
| nfile | 1 | データ・ファイルの数。今の場合はSiのデータだけなので1です。 |
| filepp(n) | filepp(1)=filplot | プロットするデータのファイル名。カッコの中のnは1からnfileまでの値をとります。 |
| weight(n) | weight(1)=1.0 | 複数のデータ・ファイルを組み合わせるときのそれぞれの重み付け |
| iflag | なし | 出力結果の次元で、2は二次元プロットです。 |
| output_format | なし | 結果をプロットするプログラムを指定。2にすれば次に出てくるplotrho.xというプログラム用のファイルを出力します。 |
| e1(i), e2(i) | なし | 2つのベクトルe1とe2を使って、電荷密度を表示する面を指定。デカルト座標で指定します。iは1から3までの値をとります。単位はalat (celldm(1)あるいはAのこと) を1とします。ベクトルe1とe2は直交している必要があります |
| nx, ny | なし | プロットする画像の解像度(ポイント数) |
最終的な結果は \begin{equation} \sum^{\mathrm{nfile}}_{n=1} \mathrm{weight}(n) \times \mathrm{rho}(n) \end{equation} で表されます。 詳しくは PP/Doc/INPUT_PP.html を参照してください。
プログラムの実行は次のように行います。
$ pp.x < Si.pp_rho.in
すると sicharge と Si.rho.dat とというファイルができます。 得られた電荷密度は plotrho.x というプログラムを使って次のようにプロットします。
$ plotrho.x
Input file > Si.rho.dat
r0 : 0.0000 0.0000 0.0000
tau1 : 1.0000 1.0000 0.0000
tau2 : 0.0000 0.0000 1.0000
read 2 atomic positions
output file > Si.rho.ps
Read 56 * 40 grid
Logarithmic scale (y/n)? > n
Bounds: 0.002452 0.075120
min, max, # of levels > 0 0.08 6
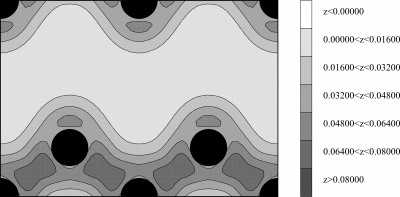
するとSi.rho.psというファイルができるので、電荷密度を確認します。
Si原子同士の間で電荷密度が大きくなっていて、Si原子間の共有結合の様子がわかります。