ホログラフィー原理とゲージ重力対応
C01班 研究分担者 関野恭弘 (拓殖大学工学部) 2023年1月28日
重力のミクロな理論であり、究極の物理法則とも言える量子重力理論は未だ完成していないが、その解明の鍵になると考えられているのが「ホログラフィー原理」という仮説である。ホログラフィー原理とは、空間のある領域における量子重力理論は、表面上の自由度を用いて定義されるべきであり、その自由度の数は1プランク面積あたり1つである、という主張である(図1参照)。(重力定数G、プランク定数ℏ、光速cの組み合わせで作られる長さのスケール![]() をプランク長という。上の記述は正確には、面積
をプランク長という。上の記述は正確には、面積![]() あたり1自由度の意味。)3次元の立体的な情報を2次元面上に記録するホログラムにちなんで、このように呼ばれている。ホログラフィー原理は、ブラックホールのエントロピーをもとに発展した考え方である。
あたり1自由度の意味。)3次元の立体的な情報を2次元面上に記録するホログラムにちなんで、このように呼ばれている。ホログラフィー原理は、ブラックホールのエントロピーをもとに発展した考え方である。
エントロピーとは、マクロな物理量で特徴づけられる系に含まれるミクロな状態数を表す量である。孤立した系では、エントロピー最大の(ミクロな状態数が最も多い)状態が平衡状態として実現される。時間発展によりエントロピーは減少しない、というのが熱力学第2法則の1つの表し方である。

図1:ホログラフィー原理のイメージ:球の内部の情報は、その表面上で、1プランク面積あたり1つの自由度で表される。
ブラックホールのエントロピー
重力の古典論(一般相対論)において、ブラックホールは、入ることは出来るが何も出ることが出来ない領域として定義される。とすると、ブラックホールに落とした物質のエントロピーは失われるのだろうか、という素朴な疑問が生じる。
ブラックホールの熱力学
1970年のBekenstein、Hawkingらの研究により、現在では、ブラックホールはエントロピーと温度を持った熱力学的な物体であると考えられている。その考え方を簡単に振り返っておく。定常状態に達したブラックホールは、質量、角運動量、電荷のみにより特徴づけられることから、熱力学で行われるような何らかの粗視化の結果として解釈できるのではないかと想像される。エントロピーが事象の地平面の面積に比例し、温度が地平面上の「表面重力」に比例するとすれば、熱力学第1法則に類似の式が成り立つ。示量性の(物質の量に比例する)量であるエントロピーを、体積ではなく面積と同一視するというのは非常に直観に反する提案だが、地平面の面積はブラックホール外部の観測者にとって明確に定義できる量であるという点が重要である(それに対して、体積の定義ははっきりしない)。さらにHawkingにより、ブラックホールは量子的には物質を吸い込む一方ではなく、有限温度の輻射と熱平衡にあることが示され、それによりエントロピーや温度が比例定数を含めて定まった。
例えば、以下の計量(以下では、光速、プランク定数、ボルツマン定数は1とする)![]() で表される、質量Mを持った漸近的平坦なSchwarzschildブラックホールを考える(
で表される、質量Mを持った漸近的平坦なSchwarzschildブラックホールを考える(![]() は2次元球面の計量を表す)。事象の地平面の半径はrS=2GMである。角運動量を持たない物質が球対称に重力崩壊してブラックホールが形成される場合を考えると、物質が分布している領域の外側はこの計量で表される。物質の部分を含めた時空の因果的構造は、図2のペンローズ図で表される。
は2次元球面の計量を表す)。事象の地平面の半径はrS=2GMである。角運動量を持たない物質が球対称に重力崩壊してブラックホールが形成される場合を考えると、物質が分布している領域の外側はこの計量で表される。物質の部分を含めた時空の因果的構造は、図2のペンローズ図で表される。
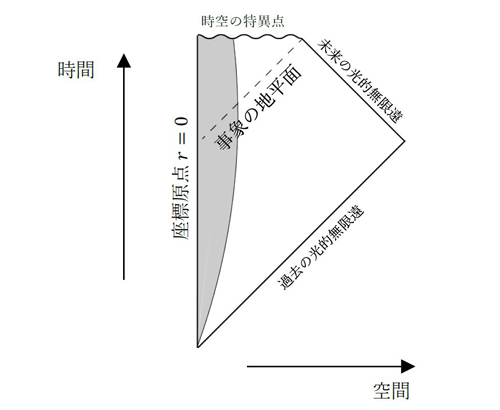
図2:物質(グレー部分)の重力崩壊により形成されたブラックホールの「ペンローズ図」。この図は時間方向と動径方向を表しており、各点に2次元球面が付随している。動径方向の光線は、上下方向から45°の直線で表される。何も光速より速く動くことはできないので、世界線が上下方向となす角度は45°以下である。よって、事象の地平面の外側から内側に入ることはできるが、一旦内側に入ると外側に出ることはできず、時空の特異点に達する。(この図では、ブラックホールの蒸発は考慮していない。)
Schwarzschildブラックホールのエントロピーは地平面の面積の1/(4G)倍の
![]() 温度は
温度は
![]() と考えられている。このように定義されたエントロピー、温度、および内部エネルギーE=Mは、第1法則dE=TdSを満たすことが分かる。
と考えられている。このように定義されたエントロピー、温度、および内部エネルギーE=Mは、第1法則dE=TdSを満たすことが分かる。
上記の温度は、例えば以下のようにして導かれる。座標変換により、地平面から外側への固有距離を表す座標ρを導入すると、地平面付近の計量(の時間と動径部分)は以下のRindler計量
![]() で表される。時間方向を解析接続
で表される。時間方向を解析接続![]() した場合、Euclid時間τの周期が4πrS以外だとρ=0は欠損角を持った特異点になるが、周期が4πrSなら特異点は無い。一般に量子統計力学で、温度はEuclid時間の周期の逆数で与えられるので、ブラックホール背景上の場の量子論は温度T=1/(4πrS)を持つことが分かる。
した場合、Euclid時間τの周期が4πrS以外だとρ=0は欠損角を持った特異点になるが、周期が4πrSなら特異点は無い。一般に量子統計力学で、温度はEuclid時間の周期の逆数で与えられるので、ブラックホール背景上の場の量子論は温度T=1/(4πrS)を持つことが分かる。
Hawkingの計算によると、平坦時空の中で物質が重力崩壊してブラックホールが出来た場合、量子的純粋状態であった初期状態が、上記の温度の熱的混合状態に発展することになる。その帰結を後ほど述べる。
一般化された第2法則とエントロピーの上限
ブラックホールが通常の意味の熱力学的物体なら、ブラックホールと外部の物質のエントロピーの合計が減少しないという「一般化された第2法則」が成り立つと考えられる。それを支持するいくつかの思考実験が考案されている。さらに、SusskindとUglumによって指摘された以下の事実は、このような合計を考えるべきであることを示唆している。場の量子論においてブラックホール外部の場のエントロピーを求める1つの方法は、地平面の向こうの自由度をトレースアウトしてエンタングルメント・エントロピーを求めることである。(自由度をトレースアウトするとは、直観的には、その自由度がとりうる状態について平均した期待値で置き換えることにあたる。エンタングルメント・エントロピーとは、量子もつれの度合いを特徴づける量。)ただし、それを試みると、地平面にいくらでも近くに自由度が存在することから、結果は発散する。一方、ブラックホールのエントロピー(地平面の面積の1/(4G)倍)への量子補正も、近距離での量子ゆらぎの寄与により発散する。このように一方だけ考えた場合、発散して意味を持たないが、それらの合計は、(繰り込まれた重力定数を使って表せば)有限な値になる。
ブラックホールのエントロピーは、一般の物質のエントロピーの上限を与えると考えられている。ブラックホールと同等のサイズ(半径)を持ち、ブラックホールより大きいエントロピーを持った物質は存在しないと考えられる。そのような物質が重力崩壊してブラックホールになったら、一般化された第2法則に反してしまうからである。エントロピーの上限は、正確にはBoussoによる「共変的な定式化」によって、一般の時空について与えられている。(エントロピーの上限は数値的には通常の物質のエントロピーに比べて大幅に大きいので、これが観測的に意義を持つことがあるかは分からない。太陽質量程度のブラックホールは半径約3kmを持ち、そのエントロピーは1077程度である。一方、太陽と同程度のエネルギーと温度を持った熱輻射のエントロピーは1067程度である。分子や原子のエントロピーは、輻射に比べて大幅に小さい。)
ブラックホールの蒸発
平坦な空間におけるブラックホールは、エネルギー(質量)が小さいほど温度が高いので、負の比熱を持つ。一般に、温度が異なる2 つの物体を接触させると、第2法則の帰結として、必ず温度の高い方から低い方に熱(エネルギー)の移動が起こる。ブラックホールの比熱が負だということは、ブラックホールの温度が熱輻射の温度より少しでも高いと、ブラックホールから熱輻射にエネルギーが移り、それによりブラックホールの温度はさらに上昇する。それを繰り返し、最終的にブラックホールは蒸発すると考えられている。
ブラックホールの形成と蒸発により、熱的な輻射のみが残り、もともとの物質の情報が失われるのだろうか(量子力学的な純粋状態が、混合状態に発展するのだろうか)、というのがブラックホールの情報問題である。質量の大きいブラックホールでは、事象の地平面の半径は大きく、曲率は小さいので、地平面近くで大きな量子重力的補正があるわけではない。また、ブラックホールがプランク長程度の大きさになったときに残った物体(「レムナント」)に何らかの量子重力的機構で全ての情報が担われるという可能性も、様々な理由から考えにくいとされている。これらのことから、情報が失われると考える研究者も多かった。しかし、基本法則において情報の損失が起こるとすると、従来の物理法則の大きな修正となる。
ホログラフィー原理
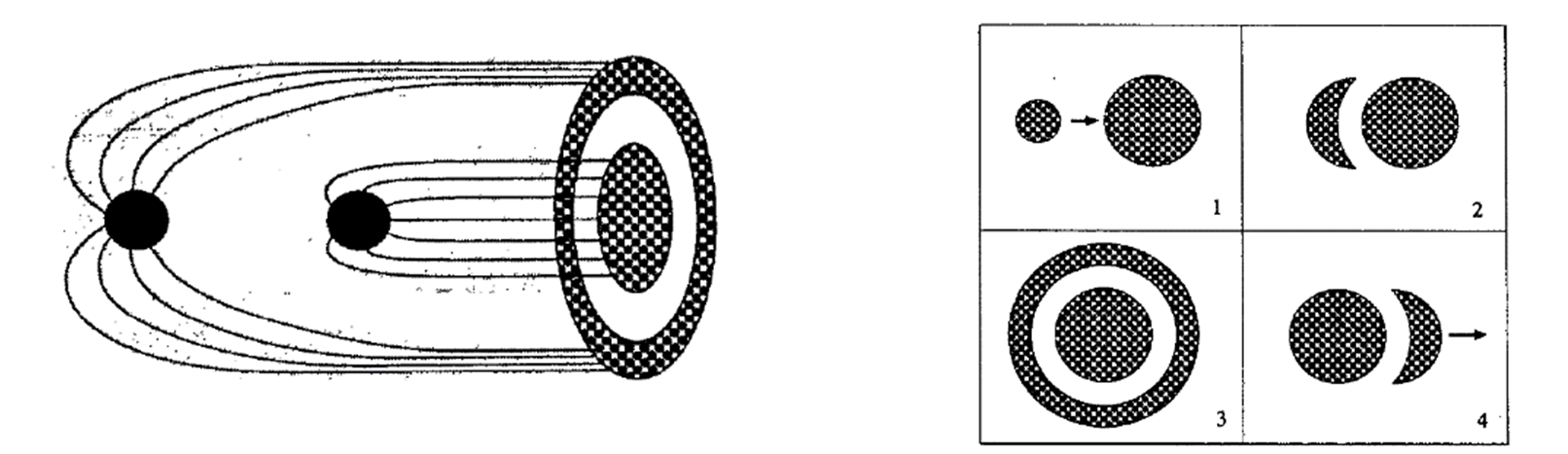
図3:3次元的な情報を2次元面に記述するメカニズムの1つの説明。左図は、2つの物体から右の2次元「スクリーン」への光線を表す。右図は、2つの物体がすれ違う(スクリーンに沿った方向の相対位置が変化する)過程をスクリーン上で見たもの。L. Susskind, “The World as a Hologram,” https://arxiv.org/abs/hep-th/9409089より、著者の許可を得て転載。
冒頭で述べたホログラフィー原理は、情報の損失が無いとする考え方である。それによると、空間領域の表面上に位置する1プランク面積あたり1つの自由度が、ブラックホールや一般の物質のエントロピーの微視的意味を与えることになる。
空間内部の情報が具体的にどうやって表面上の自由度によって担われるかは、後述のゲージ重力対応において部分的には分かってきているが、解明の途上である。ここでは一例として、Susskindによる初期の論文で挙げられている1つの説明を挙げておく。空間内部に物体が存在するという情報は、物体から出て、情報を記録する面(スクリーン)に垂直に入射する光線を用いて、光線と面の交点に記録される(図3参照)。複数の物体がある場合も、重力による光の湾曲により像が重なることはない。
ブラックホールの外部の観測者にとって、ブラックホールは地平面上の自由度によって記述されることになる。あるいは、地平面のわずかに外側に位置する時間的な面(stretched horizon)を考えることもある。ホーキング輻射はその自由度の一部が外部に放出されたものと考えられる。純粋状態にある系を部分系AとBに分けて、例えばBがAに比べて非常に大きい場合に部分系Bをトレースアウトすると、全系が典型的な状態にあるなら、部分系Aの状態を表す密度行列は最大限にランダムな混合状態になることが知られている。Hawkingの計算で得られた熱的なスペクトルは、そのような性質のものだと考えられる。
上で述べたように、大きなブラックホールの地平面上では曲率が強いわけではないので、地平面上に、古典論からは理解できない量子重力の基本的自由度が存在するというのは不思議に感じられるかもしれない。しかし、地平面の近くで静止している物体は、大きな加速度とエネルギーを持っている。地平面外部の観測者による記述では、そのような高エネルギーのモードが必要になるので、このようなことがあり得ると考えられる。
ブラックホールの「相補性」
ホログラフィー原理と密接に関わる考え方に、ブラックホールの(あるいは、一般に、地平面の)「相補性」がある。これは、量子重力理論は、1人の観測者がアクセスできる自由度を用いて記述されるべきであり、その理論が他の領域の情報も含んでいるという考え方である。(これは、量子力学における、位置と運動量の相補性にちなんで名付けられた言葉である。量子力学では、状態は、位置か運動量どちらか一方により指定されるので、両方を指定することはできず、一方を指定すれば原理的には他方が分かる。それと同様に、ブラックホールの外部が分かれば内部も分かることを意味している。)地平面の向こうの情報が地平面を超えて漏れてくることは因果的にあり得ないので、情報損失という結論を回避するには、ホログラフィー原理に加えて相補性が必要だと思われる。
ただし、相補性はホログラフィー原理に劣らず直観に反する主張であり、その正当性は詳しく検討されるべきだろう。その一例として、以下のような思考実験がある(図4参照)。ブラックホールに落下する人(Alice)と外部で留まっている人(Bob)を考える。Bobは、Aliceが地平面を越えた後しばらくHawking輻射を集めてAliceの量子情報を再構成し、その後、自分も地平面の向こう側へ行き、Aliceから直接信号を受けとる。もし、この操作によりBobがAliceの量子状態の複製を作ることが出来るなら、量子力学の線形性の帰結である非クローン定理(量子論では、任意の未知の状態を複製する操作は不可能であるという定理)が破れることになってしまう。HaydenとPreskillは、量子情報理論の技術を用いてこの問題を検討し、以下の事実を指摘した。ブラックホールが形成されてから放出されたHawking輻射をBobが全て保持していたとして、それとAliceが地平面を越えた後に放出されたHawking輻射とのエンタングルメントを利用すると、非常に素早く(Aliceの持っている量子ビットと同程度の量の輻射を得るだけで)Aliceの情報を再構成できる。この手法では、Aliceの情報が地平面上の自由度と混ざって(スクランブルして)典型的な状態になっていることを仮定している。したがって、Aliceの情報が放出されるまでの時間スケールは、従来考えられていたようにブラックホール全体が蒸発するまでの時間ではなく、地平面上での情報のスクランブリングに必要な時間で決まる。その時間スケールは、ブラックホールの幾何学的な構造の解析からBobが特異点に到達する前にAliceから情報を得ることをちょうど禁止するだけの長さであることが分かった。地平面上でのスクランブルの早さは、通常の局所的な場の理論よりも早いので、「早いスクランブリング」と呼ばれている。これが自然界で最も早い情報のスクランブルであることが、関野とSusskindにより予想されている。
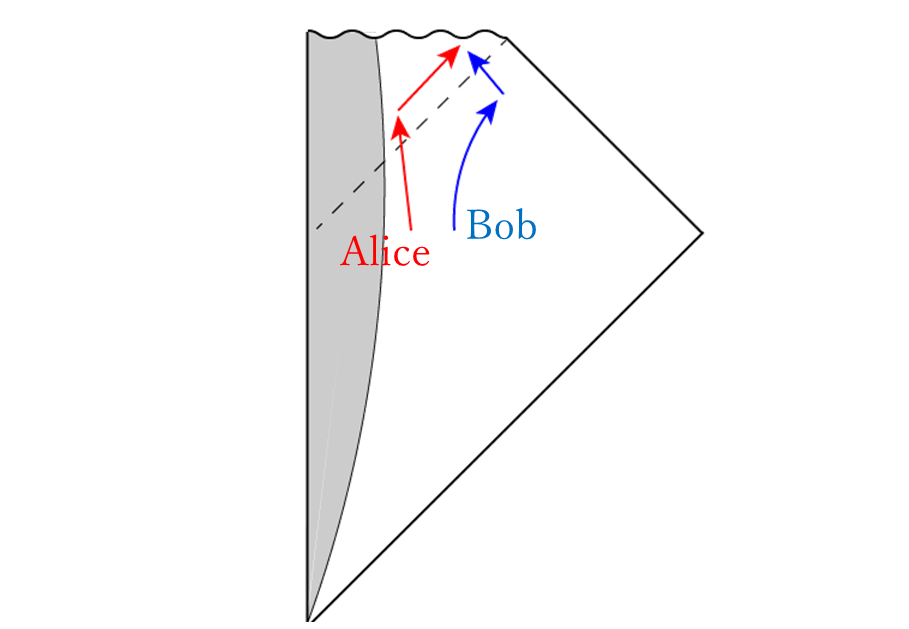
図4:ブラックホールにおける思考実験。Bob(青い矢印)は、Alice(赤い矢印)が地平面を越えた後しばらくHawking輻射を集めてAliceの量子情報を再構成し、その後、自分も地平面の向こう側へ行き、Aliceから直接信号を受けとる。これが可能だと量子力学の非クローン定理に反するが、AliceとBobが時空の特異点に到達する前にこれを行う事は不可能であることが示されている。
なお、この思考実験で現れるような、一般相対論における基準系の取り換えにあたる変換が、厳密な量子重力理論(後述の行列自由度を持った理論等)で具体的にどのように表されるかは未解明の問題である。しかし、最近の研究によってホログラフィー原理の特別な例であるゲージ重力対応における量子情報量(エンタングルメント・エントロピー)の具体的な計算によって、ブラックホールの蒸発では情報の損失が起こらない強い証拠が得られるようになった。その詳細は、別稿で詳しく説明するが、以下では、ゲージ重力対応について解説したい。
ゲージ重力対応
ホログラフィー原理の具体的実現と考えられているのが、1997年にMaldacenaによって提唱された「AdS/CFT対応」である。これは、反ドジッター(Anti-de Sitter: AdS)空間の上の超弦理論は、その境界(空間的無限遠)で定義された、重力を含まないゲージ理論(共形不変な場の理論、すなわち共形場理論:Conformal Field Theory)と等価であるという予想である。共形不変性とは、理論が局所的なスケール変換(等角写像)により不変であることを言い、2次相転移の臨界点などで現れる。共形場理論における物理量(演算子)を特徴づける際、スケーリング次元(相関関数が距離の何乗に比例するか)が本質的な役割を果たす。AdS空間や共形不変性な理論に限らずより一般に、超弦理論(あるいは量子重力理論)と境界上のゲージ理論との対応を「ゲージ重力対応」という。
AdS空間(AdS宇宙)
AdS空間は負の宇宙定数を持った時空である。(d+1)次元時空は、大域的座標と呼ばれる座標系を用いて、以下の計量
![]() で表される(
で表される(![]() は(d-1)次元球面Sd-1の計量を表す)。時間一定面は無限の体積を持ち、ρ→∞に位置するSd-1が境界にあたる。AdS空間の因果的構造は図5で表される。円柱の高さ方向が時間t、円柱の中心軸が原点ρ=0、側面が境界を表す。境界Sd-1をここでは円周として表している。図2と同様、動径方向の光線は、上下方向に対して45°の直線で表される。動径方向の重力の有効ポテンシャルのため、質量を持った場(粒子)は境界に達することが出来ないが、質量ゼロの場は有限時間で境界に達することが出来る。そのため、AdS空間内部のダイナミクスを記述するには、境界で何らかの境界条件が必要である。
は(d-1)次元球面Sd-1の計量を表す)。時間一定面は無限の体積を持ち、ρ→∞に位置するSd-1が境界にあたる。AdS空間の因果的構造は図5で表される。円柱の高さ方向が時間t、円柱の中心軸が原点ρ=0、側面が境界を表す。境界Sd-1をここでは円周として表している。図2と同様、動径方向の光線は、上下方向に対して45°の直線で表される。動径方向の重力の有効ポテンシャルのため、質量を持った場(粒子)は境界に達することが出来ないが、質量ゼロの場は有限時間で境界に達することが出来る。そのため、AdS空間内部のダイナミクスを記述するには、境界で何らかの境界条件が必要である。
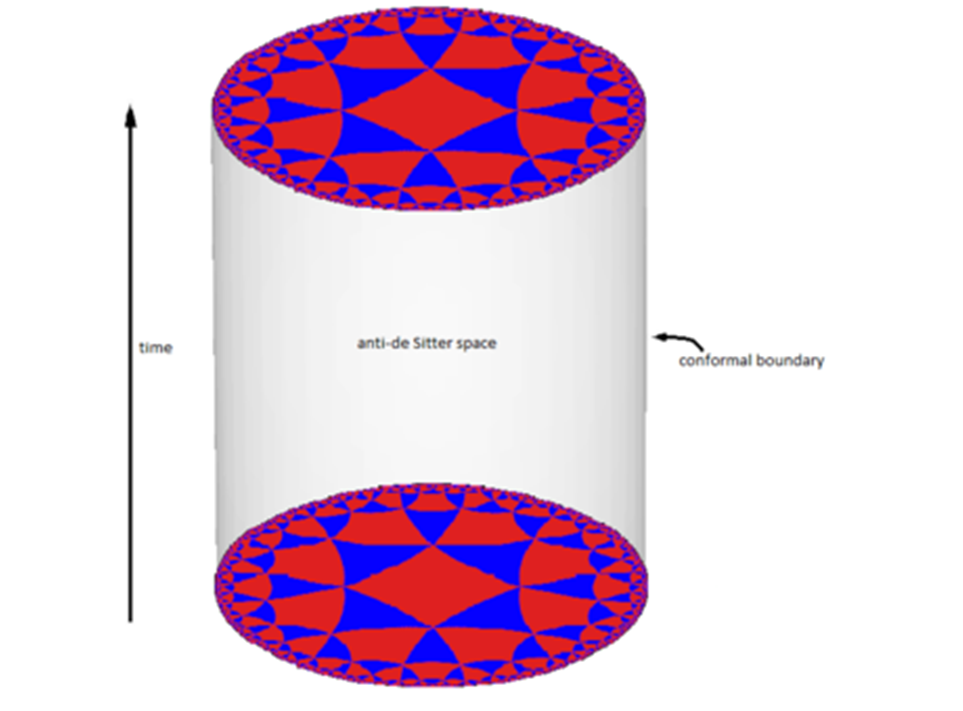
図5:AdS空間の因果的構造。Wikipedia ”AdS/CFT対応“より。©Polytope24 (Licenced under Creative Commons, CC BY-SA 3.0)
AdS/CFT対応の第1の根拠は、両理論の対称性が一致することである。(d+1)次元AdS空間は、1次元高い平坦時空Rd,2内の双曲面として表現できることから、SO(d,2)対称性を持つ。この対称性はd次元時空での共形対称性と同型である。例えば、AdS空間内部のある点を動径方向に動かすような変換は、境界上のスケール変換(拡大縮小)にあたる。(この変換は、例えば、図5の1つの模様を同じ形の拡大された模様に移す)。
Dブレーンの2通りの記述
AdS/CFT対応は、超弦理論におけるDブレーンの2通りの記述がもとになっている。最も典型的な例であるD3ブレーンの場合を考える。量子重力理論の最有力候補として知られる超弦理論は、物質の最小単位が粒子(素粒子)ではなく、実は弦(ひも)と考えることで構築される理論である。この弦は非常にサイズが小さく、我々が実験などで通常、観測するエネルギースケールでは粒子と区別ができない。しかし、その微細な弦の構造によって、重力理論の量子化で生じる紫外発散の困難を解消することができる。この弦には2種類あり、輪ゴムのような「閉じた弦」と、それを半分に切り、両端点がある「開いた弦」である。この超弦理論でブラックホールのように非常に重い物体としてDブレーンがある。
Dpブレーンとは、超弦理論の予言する10次元時空において、p次元的な空間的広がりを持ったソリトン的物体である。Dブレーンは開いた弦の端点が位置することができる場所として定義され、開いた弦の振動モードがDブレーンの運動の自由度を表している。一方、開いた弦のループが閉じた弦となることにより、Dブレーンは、閉じた弦を放出したり吸収したりできる。重力子は閉じた弦の固有振動モードの1つである。
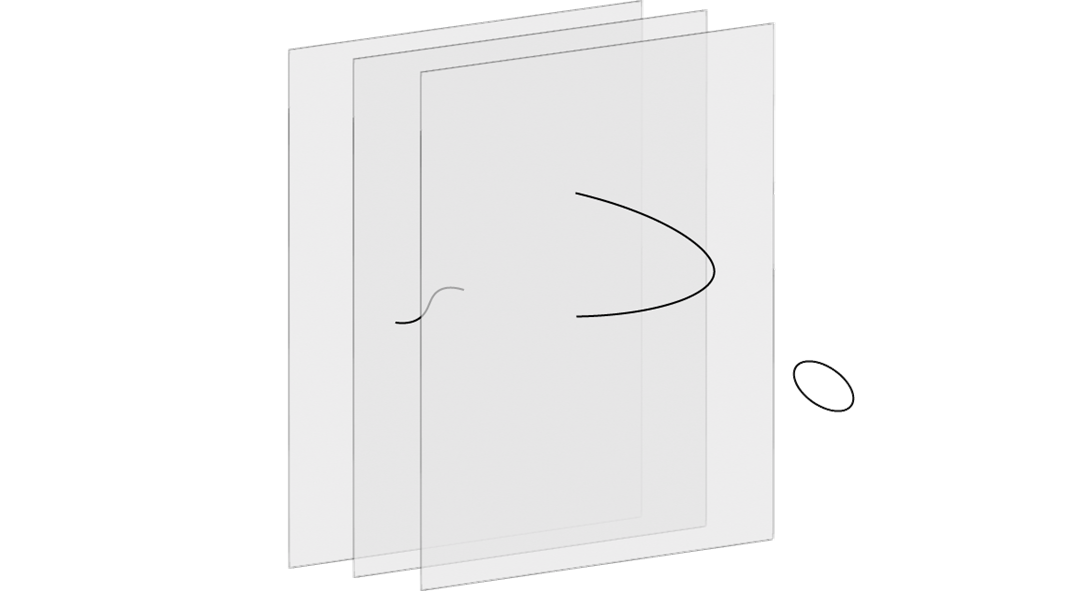
図6:Dブレーンと弦。複数(ここでは3枚)のDブレーンがある場合、開いた弦には、同じDブレーンをつなぐものと異なるDブレーンをつなぐものがある。閉じた弦はDブレーンから離れて存在できる。
Dブレーンを重力場(およびゲージ場やディラトン場)の源として考え、超重力理論(超弦理論の低エネルギー極限)の古典解として表すのが1つの方法である。これは、閉じた弦の質量ゼロのモードを用いた記述であり、弦の長さ(ストリングスケール)lsに比べて長距離で有効な記述である。D3ブレーン解の近地平面極限(平坦時空に漸近する遠方の領域を無視して、ブレーンの近くに着目する極限)をとると、AdS5×S5の形になる。5次元球面S5は、D3ブレーンの4次元世界面に垂直な6次元空間の角度方向を表している。
一方、lsより近距離の現象は、開いた弦の最低次(質量ゼロ)のモードにより記述できると考えられている。これは、張力![]() の弦が長さΔxを持っているときのエネルギーが
の弦が長さΔxを持っているときのエネルギーが![]() であることから、長さΔx<lsの最低次モードのエネルギーは、励起モードのエネルギー1/lsより小さいためである。N枚のDpブレーンの集まりの近距離における記述は、超対称を持った (p+1)次元SU(N)ヤンミルズ理論で与えられる。この理論は、矛盾なく定義できる最大の超対称性を持った、非常に対称性の高い理論であり、(p+1)次元ゲージ場の他にボソン場として (9-p)個のスカラー場を含む。これらのゲージ場やスカラー場はN×Nエルミート行列で表され、ゲージ群SU(N)の随伴表現に属する。スカラー場の対角要素は同じDブレーンをつなぐ弦の自由度であり、1つ1つのDブレーンの位置を表す。非対角要素は異なるDブレーンをつなぐ弦から現れる超弦理論特有の自由度であり、SU(N)ゲージ対称性は、ボソンやフェルミオンの同種粒子の交換対称性を一般化した新奇な対称性である。Dpブレーンを記述する(p+1)次元ヤンミルズ理論の結合定数gYMは、弦の結合定数gsと
であることから、長さΔx<lsの最低次モードのエネルギーは、励起モードのエネルギー1/lsより小さいためである。N枚のDpブレーンの集まりの近距離における記述は、超対称を持った (p+1)次元SU(N)ヤンミルズ理論で与えられる。この理論は、矛盾なく定義できる最大の超対称性を持った、非常に対称性の高い理論であり、(p+1)次元ゲージ場の他にボソン場として (9-p)個のスカラー場を含む。これらのゲージ場やスカラー場はN×Nエルミート行列で表され、ゲージ群SU(N)の随伴表現に属する。スカラー場の対角要素は同じDブレーンをつなぐ弦の自由度であり、1つ1つのDブレーンの位置を表す。非対角要素は異なるDブレーンをつなぐ弦から現れる超弦理論特有の自由度であり、SU(N)ゲージ対称性は、ボソンやフェルミオンの同種粒子の交換対称性を一般化した新奇な対称性である。Dpブレーンを記述する(p+1)次元ヤンミルズ理論の結合定数gYMは、弦の結合定数gsと![]() の関係がある。D3ブレーンを記述するヤンミルズ理論は、結合定数が無次元であるだけでなく、ベータ関数(量子効果のスケール依存性)が厳密にゼロであり、共形不変性を持つ。
の関係がある。D3ブレーンを記述するヤンミルズ理論は、結合定数が無次元であるだけでなく、ベータ関数(量子効果のスケール依存性)が厳密にゼロであり、共形不変性を持つ。
Dブレーンの枚数Nが多い場合、上記の2つの記述に共通の有効領域があるのではないか、というのがAdS/CFT対応の根拠である。古くから知られているように、’t Hooft結合定数![]() を固定した大N極限(’t Hooft 極限)では、ゲージ理論の摂動展開のFeynmanダイアグラムは、ダイアグラムにより作られる2次元面のトポロジーに応じて分類される。各ダイアグラムの寄与が2次元面の種数(genus)に応じた1/Nの因子を持つことから、1/Nを弦の結合定数とした弦の理論としてゲージ理論の1/N展開を表すことができるのではないかと考えられていた。AdS/CFT対応はその1つの具体化であると言える。
を固定した大N極限(’t Hooft 極限)では、ゲージ理論の摂動展開のFeynmanダイアグラムは、ダイアグラムにより作られる2次元面のトポロジーに応じて分類される。各ダイアグラムの寄与が2次元面の種数(genus)に応じた1/Nの因子を持つことから、1/Nを弦の結合定数とした弦の理論としてゲージ理論の1/N展開を表すことができるのではないかと考えられていた。AdS/CFT対応はその1つの具体化であると言える。
’t Hooft極限では弦の結合定数は小さく、弦のループは無視できる。N枚のD3ブレーンの近地平面極限の時空![]() において、AdS5およびS5は同じ曲率半径
において、AdS5およびS5は同じ曲率半径![]() を持つ。よって、’t Hooft 結合
を持つ。よって、’t Hooft 結合![]() が大きい場合は、時空の曲率半径Rがlsに比べて十分大きい場合にあたる。このときは、1/lsに比例したエネルギーを持つ弦の励起モードの効果が無視できて、超弦理論の低エネルギー近似である超重力理論による記述が有効である。その反対に、’t Hooft 結合が小さい場合は、時空が強く曲がっている場合にあたり、弦の励起状態の効果が無視できないと考えられる。このように、AdS/CFT対応(あるいは一般にゲージ重力対応)は、一方の理論の解析が簡単(例えば、超弦理論に対して超重力理論による近似が可能)なとき、他方の理論の解析が難しい(ゲージ理論の有効結合定数である’t Hooft 結合が強い)という、「強結合/弱結合双対性」の側面がある。
が大きい場合は、時空の曲率半径Rがlsに比べて十分大きい場合にあたる。このときは、1/lsに比例したエネルギーを持つ弦の励起モードの効果が無視できて、超弦理論の低エネルギー近似である超重力理論による記述が有効である。その反対に、’t Hooft 結合が小さい場合は、時空が強く曲がっている場合にあたり、弦の励起状態の効果が無視できないと考えられる。このように、AdS/CFT対応(あるいは一般にゲージ重力対応)は、一方の理論の解析が簡単(例えば、超弦理論に対して超重力理論による近似が可能)なとき、他方の理論の解析が難しい(ゲージ理論の有効結合定数である’t Hooft 結合が強い)という、「強結合/弱結合双対性」の側面がある。
ホログラフィー原理との整合性
ゲージ理論の自由度がホログラフィー原理に適合していることが、SusskindとWittenにより以下のように説明されている。AdS空間の境界の面積は無限大なので、赤外(IR)カットオフを導入する。また、連続的な空間で定義されているゲージ理論の自由度の数も無限大なので、格子上で定義する等により紫外(UV)カットオフを導入する。これらのカットオフが以下のように関係していると考える。ここでは簡単のため、(4+1)次元AdS空間を「Poincare座標」
![]() によって表す(i =1,…,3)。この座標系は、大域的座標系で書いたAdS時空の一部を覆っていると見ることも、大域的AdSの境界上の1点の近傍を拡大したと見ることもできるが、ここでは後者の見方をとる。動径座標z =0が境界を表している。
によって表す(i =1,…,3)。この座標系は、大域的座標系で書いたAdS時空の一部を覆っていると見ることも、大域的AdSの境界上の1点の近傍を拡大したと見ることもできるが、ここでは後者の見方をとる。動径座標z =0が境界を表している。
境界上のUVカットオフΔx≥ϵがIRカットオフΔz≥ϵに対応すると考える(その1つの説明は、図7参照)。すると、ゲージ理論の格子点1つ(Δx∼ϵ程度の大きさの領域)は、AdS空間で面積![]() (すなわち、単位AdS面積)を持つことになる。ここで、5次元プランク長lPは5次元Einstein-Hilbert作用の係数が
(すなわち、単位AdS面積)を持つことになる。ここで、5次元プランク長lPは5次元Einstein-Hilbert作用の係数が![]() であるとして定義される。また、5次元理論は10次元Einstein-Hilbert作用をS5方向にコンパクト化することにより得られ、10次元Einstein-Hilbert作用の係数は
であるとして定義される。また、5次元理論は10次元Einstein-Hilbert作用をS5方向にコンパクト化することにより得られ、10次元Einstein-Hilbert作用の係数は![]() であることから、
であることから、
![]() である。よって、AdS半径
である。よって、AdS半径![]() より、
より、
![]() (単位AdS面積は、プランク面積のN2倍)が成り立つ。つまり、1つの格子点にオーダーN2個の自由度を持つSU(N)ゲージ理論は、プランク面積あたり1自由度というホログラフィー原理に合致している。
(単位AdS面積は、プランク面積のN2倍)が成り立つ。つまり、1つの格子点にオーダーN2個の自由度を持つSU(N)ゲージ理論は、プランク面積あたり1自由度というホログラフィー原理に合致している。
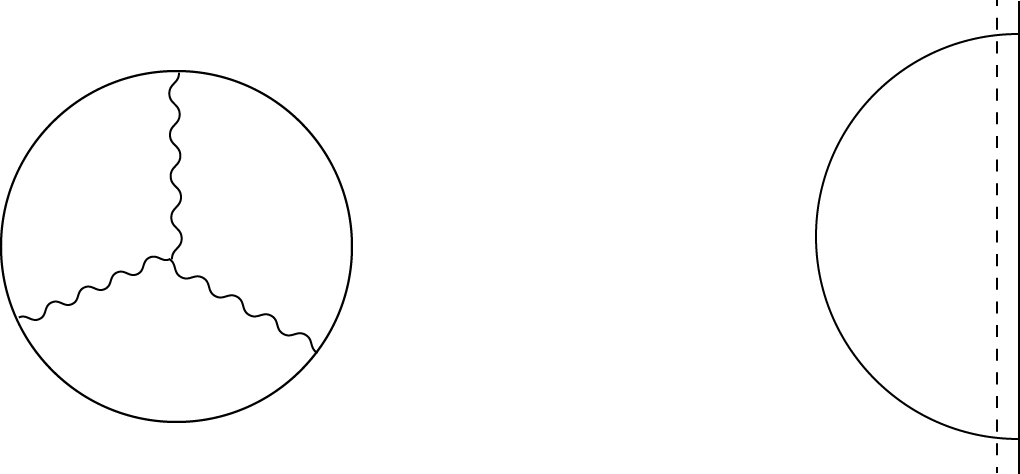
図7:(左) AdS/CFT対応でゲージ理論の相関関数を求める際に現れる「Wittenダイアグラム」。円がEuclid化されたAdS空間、円周が境界を表す。(右)ゲージ理論の2点関数に対する測地線近似。右端の実線が境界(z=0)、破線がカットオフ(z=Δz=ϵ)を表す。
ゲージ重力対応における物理量の対応
空間内部(超弦理論、あるいは超重力理論)と境界(ゲージ理論)の物理量の間の関係が、Gubser-Klebanov-PolyakovおよびWittenによって提案されている。それによると、AdS上の場を![]() 、それに対応するゲージ理論の演算子をO(x)としたとき、
、それに対応するゲージ理論の演算子をO(x)としたとき、
![]() が成り立つ。左辺は、AdSの境界での境界条件
が成り立つ。左辺は、AdSの境界での境界条件![]() =
=![]() 0 (x)の汎関数としての量子重力理論の分配関数である(
0 (x)の汎関数としての量子重力理論の分配関数である(![]() は
は![]() についての経路積分を表す)。右辺は、ゲージ理論における演算子O(x)の相関関数の生成汎関数である(xは境界に沿った座標を表す)。AdS空間での場の質量が、ゲージ理論の演算子のスケーリング次元に対応する。上の式を用いて、’t Hooft 結合が大きい大N極限におけるゲージ理論を、超弦理論(あるいは超重力理論)の古典論により計算する研究が盛んに行われた。
についての経路積分を表す)。右辺は、ゲージ理論における演算子O(x)の相関関数の生成汎関数である(xは境界に沿った座標を表す)。AdS空間での場の質量が、ゲージ理論の演算子のスケーリング次元に対応する。上の式を用いて、’t Hooft 結合が大きい大N極限におけるゲージ理論を、超弦理論(あるいは超重力理論)の古典論により計算する研究が盛んに行われた。
超重力理論を用いた摂動的な計算は、Euclid化した空間で、境界と空間内部をつなぐプロパゲーターを用いて行われ、図7(左)のような「Wittenダイアグラム」で表される。質量の大きい場合に有効な測地線近似を考えるのも、直観的に有用である。AdS空間の境界上の2点をつなぐ測地線はPoincare座標を用いると図7(右)のように半円で表される。よって、境界に沿った方向の間隔Δxが、どれだけAdS空間の内部まで探索されるかを表す動径座標距離Δzを決めている。上で述べたUVとIRのカットオフの関係もこれに基づいている。
AdS上の超弦理論を厳密に解くのは困難だが、半古典近似により、弦に特徴的な様々な物理量が計算され、強結合ゲージ理論の物理量として解釈されている。例えば、S5方向に運動量を持った点粒子状態の近傍での弦の励起状態の解析や、AdS内で図8(左)のように、伸びて折りたたまれて回転している弦を表す古典解の解析が行われ、強結合ゲージ理論における量子数が大きい演算子の相関関数が求められた。また、ゲージ理論のWilsonループの期待値は、図8(右)のように、Euclid計量を持ったAdS空間上で、境界上のループに端を持つ弦の世界面の作用を評価することにより与えられる。
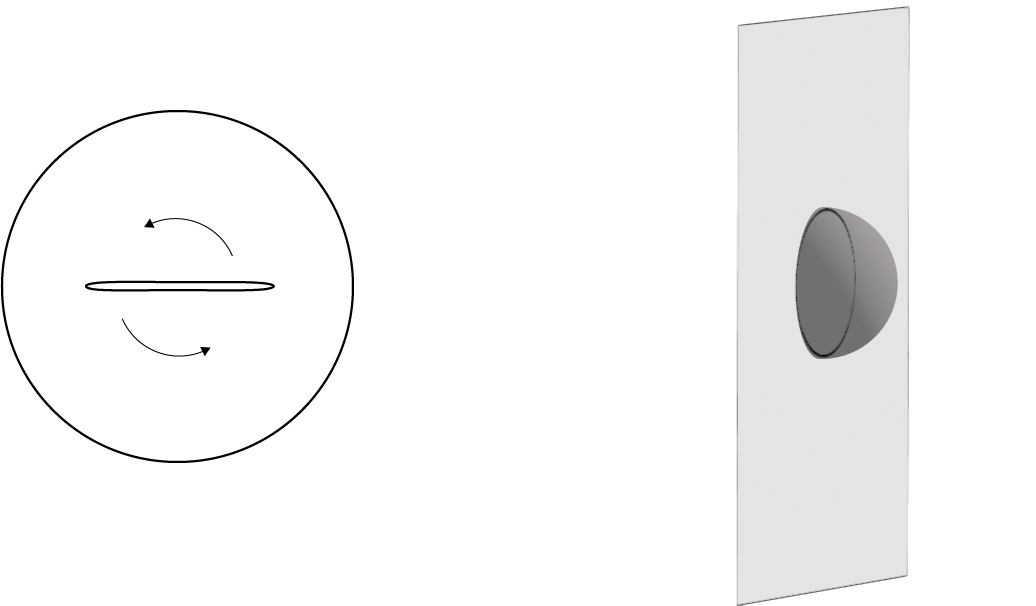
図8:(左)AdS空間内で折りたたまれて回転する弦。この図はAdS空間内の時間一定面を表し、円周は境界を表す。(右)ゲージ理論のWilsonループの期待値は、境界上のループに端を持つ弦の世界面を用いて計算される。
有限温度の相転移
漸近的AdSの時空においては、背景時空上の場だけでなく、時空自体が、境界における境界条件に応じてEuclid計量の経路積分によって決まる。作用の停留点が古典的な寄与を与えるが、それが複数ある場合、相転移の可能性がある。境界条件として、Euclid化された時間方向の周期(温度の逆数)をβ、境界Sd-1の半径をβ'とする(それぞれに対する共通の因子に意味は無く、比β/β'にだけ意味がある)。低温(大きいβ/β')での時空は、「有限温度AdS空間」(大域的座標を用いたAdS空間でEuclid時間を周期的にしたもの)だが、あるβ/β'で相転移が起こり、高温では「AdS-Schwarzschildブラックホール解」が支配的になる。この事実は、4次元時空の場合にはHawkingとPageの研究により知られていた。この相転移は、ゲージ理論におけるクォーク閉じ込め/非閉じ込めの相転移にあたる。
未解明の課題
上で述べたように、曲率の弱い背景時空上での超弦理論と強結合ゲージ理論の間の対応に関する研究がこれまで盛んに行われてきた。ここでは、D3ブレーンに関連する場合を主に述べたが、その他、超弦理論に直接関係しない場合を含む様々な場合に同様の研究が行われており、ゲージ重力対応は、原子核理論、物性理論を含む強結合量子系の新たな研究手法と見なされつつある。
ただ、ゲージ重力対応の証明は無い。そのため、どのような場合に対応が成り立つのかは明らかでなく、重力理論とゲージ理論の変数の間の具体的な対応も特殊な場合以外分かっていない。上記の極限と反対の、曲率が強い時空上の超弦理論と弱結合ゲージ理論との対応に関しては非常に研究が少ないが、ゲージ重力対応の証明に向けては、この領域の理解も重要だと思われる。
また、平坦時空や正の宇宙定数を持った時空に対するゲージ重力対応がどのようなものかは明らかでない。現実の宇宙は平坦に近いが、宇宙定数が微小な正の値をとることが観測から知られており、宇宙初期にも、近似的に正の宇宙定数を持つと見なすことができる「インフレーション」(急激な加速膨張期)があったと考えられるので、ゲージ重力対応をAdS空間以外に一般化していくことは重要な課題である。
AdS/CFT対応におけるホログラフィー原理の議論で見たように、AdS面積内の物理はN2個の行列自由度によって表されるので、平坦時空(AdS半径が無限大にあたる)は行列自由度を用いて記述されることが自然に予想される。行列の相互作用においては、どの行列要素も他のどの行列要素とも相互作用するという意味で、これは非常に非局所的な理論であることが示唆される。
正の宇宙定数を持ったドジッター(de Sitter: dS)空間は、時間的な境界が無いという点でAdS空間と大きく異なる。ドジッター空間には、時間的な境界が無い代わりに、無限の未来に空間的な境界があり、これにホログラフィー原理を適用すると、ドジッター空間の重力理論は、時間軸を含まないユークリッド空間で定義された共形場理論に対応する、というdS/CFT対応が得られる。しかし、AdS/CFT対応とは異なり、時間を含まない理論から、時間を含む重力理論が創発することになり、dS/CFT対応は直観的な理解ですらはるかに難しい。そのせいで、dS/CFT対応の研究は未だに発展途上にある。また最近では、別の考え方として1人の観測者にとっての事象の地平面(宇宙論的な地平面)で定義すべきであるという提案もなされている。
新しい展開:量子情報理論とゲージ重力対応の深い関わり
AdS/CFT対応は、これまで非常に多くの成功を収めてきたが、それがどのようなメカニズムで生じるのかという基礎原理は、現在でも未解明であり、ブラックボックスと言える。ゲージ重力対応をAdS空間を超えて、現実的な宇宙に拡張するためにも、この基礎的な問題は避けて通ることができないと思われる。しかし、最近の研究の進展で、ゲージ重力対応の基礎原理に量子情報理論が深く関係することが分かり、多くの成果が得られている。その発端となったのが、「笠-高柳公式」である。この公式は、「量子情報の量(エンタングルメント・エントロピー)が、AdS空間の断面積(正確には極小曲面の面積)に等しい」、ことを表し、重力理論の宇宙が量子情報の集合体であると解釈できることを示唆する。この最近の新しい考え方については、別稿で詳しく解説される予定である。
