テンソルネットワークとダイヤグラム
D02班 研究代表者 奥西 巧一 (新潟大学自然科学系(現:大阪公立大学大学院理学研究科))
2025年3月26日(ニュースレターより転載)
極限宇宙では量子情報分野の発展を媒介にした素粒子・宇宙・物性などの多様な物理分野にわたる融合研究の展開をめざしていますが、その交点に位置する重要なキーワードの一つが、テンソルネットワーク(TN)です。TNとは、ひとことで言ってしまえば、非常に多くの自由度が複雑に絡み合う量子多体状態を、小さなテンソルに分解・ネットワーク状に再結合して表現する系統的な記述法、および、その近似的な数値計算技法を指しますが、異分野融合のキーワードということは、その説明の切り口も色々あるということになります。TNにおける最適化と量エンタングルメントの関係や基本的なテンソルの操作については、すでに十分な解説[1]やパッケージ[2]等もあることから、ここでは、スタンダードなものとは少し異なる観点からその理論構造を論じてみたいと思います。
TN法の解説を開くと、理屈より先にまず目に飛び込んでくるのが、多様なダイヤグラムだと思います。図1はいくつかの典型的な例になりますが、1+1次元系なら行列積状態(MPS)、2+1次元ならPEPS/TPSとか呼ばれる状態、1+1次元の量子臨界系なら階層構造をもつMERAがよく見かけるものだと思います。個々の色付シンボルがテンソルを、そこから延びる脚がそのテンソルに係る自由度を表しています。これらの例では、基本的に対象となる量子多体系の性質や格子の形状を反映したネットワーク構造を持ちますが、TNを量子計算の古典計算機による近似計算に用いる場合は、一般に、そのネットワーク構造は複雑になることが多いです。いずれにしても、複雑に絡み合うテンソルの脚の縮約を、テンソルの間の結線により直感的にとらえられるので、ダイヤグラムは大いにTNの理解の助けになるとともに、ミスの混入防止にも役立ち、広く用いられるようになりました[3]。ただし、適当に分解するだけでは計算精度を担保できる良いTNにはなりません。量子多体系や量子回路に埋め込まれたエンタングルメントを指標にネットワーク構造やテンソルの最適化を実装する必要があるのですが、図中の例に対しては多くの人の検証を経た定評のあるアルゴリズムが構成されています。
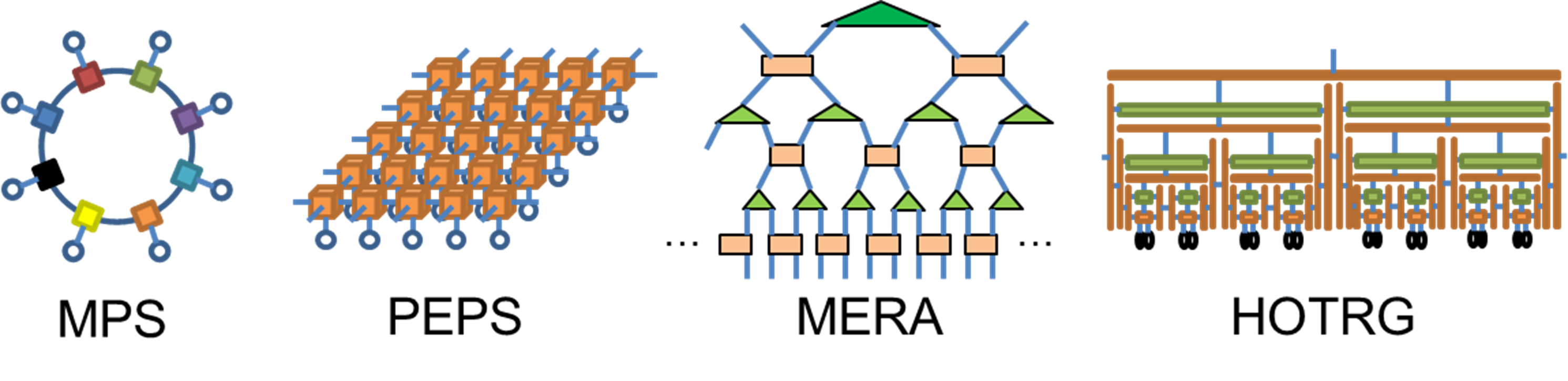
図1:典型的なテンソルネットワーク図形の例
さて、一方で、理論物理学において、似たようなダイヤグラムを使って効率よく計算を行うツールとして、やはりファインマン図形を避けて通ることはできません。とくに量子多体問題においては、複雑な摂動計算の一般項を規則に従って図形を並べることで視覚的に表すことができるとともに、その図形の個々のパーツも粒子の伝搬や散乱を表すので物理的な意味も非常に掴みやすくなります。非摂動効果が強調される場面も多いですが、それでもファインマン図形を使った物理的プロセスの理解は、量子多体系の記述に基本的な役割を果たしてきたといえます。ファインマン図形もTNのダイヤグラムも、複雑な多体効果を系統的に記述するために便利に用いられているわけですが、違いはどこにあるでしょうか? 両者を対比しながら考察することは、TNの特徴を理解する上で大変有益です。
まず、ファインマン図形の方ですが、これはハミルトニアン(もしくはラグラジアン)を書き下せば、その非摂動項と摂動項の関係ですべての図形が自動的に規定されてしまいます。非摂動項が自由粒子で、その相互作用による散乱とそれを繋ぐ伝搬関数の組み合わせで図形を表し、相関関数という期待値レベルの物理量を計算することが通常です。さらに、Wilson型くりこみ群では高エネルギーのモードの部分和を取りながら徐々に作用を変形し、エネルギースケールに応じた準粒子や有効相互作用の表現を追いかけていきますが、現れる図形という意味では、結局、準粒子描像にもとづいた表現で、「粒子の相互作用項→対応する図形」の順で規定されてしまうことになります。すなわち、図形中にTNと同様なパーツが並びますが、ネットワークの形状そのものは自由に操れるわけではありません。また、くりこみ群変換の中には、基底を組み替える際に変分的要素が入らないことも押さえておくべき点です[4]。
TNでは上記の順序が逆転します。まずネットワークを準備し、その後でネットワーク中の個々のテンソルを変分最適化することになります。例えばMPSや、より一般に樹状テンソルネットワーク(TTN)では、波動関数を特異値分解することで得られる特異値を指標として“最良”な基底を系統的に構成することが可能です。特異値分解を用いたやり方は部分系間のエンタングルメントエントロピーの最大化と言い換えることもできます。ネットワーク中の各所で最適な基底が変遷するため“粒子の散乱”のような直感的に分かりやすい表現になりませんが、特異値が部分系の間にまたがるベル対のおおよその分布に相当することから、量子情報分野との関係性がより明確になります。さらに、図2のように、テンソルを部分的にくり抜いたテンソルネットワークを裸のスピンから穴に現れる補助自由度への変換とみなすと、ハミルトニアンに対する固有値問題を、有効ハミルトニアンと、くり抜いた穴にはまる“波動関数テンソル”の変分問題に書き換えることができます。このため、TNにはくりこみ群的な粗視化された補助自由度への変換という思想が常につきまといます。実際に密度行列くりこみ群(DMRG)ではの対角化を経由してを逐次的に構成したため、“RG”が冠された経緯があります。しかし、スケール変換をともなうWilson型くりこみ群変換として解釈するには、ネットワークに階層性が必要です。図1中のMPSでは、ネットワークが線形に延びるだけでスケール性は変わらないので、Wilson型のくりこみ群と直接的な対応をつけることはできません。DMRGの初期ではこの点についての理解が不十分だったため混乱が生じました。一方で、MERAやHOTRGはスケール階層性のあるネットワークを持つため、固定点テンソルのスペクトルを解析することでスケール次元等も系統的に評価できます[5]。いずれせよ、見たい物理を表現するために柔軟にネットワークの形を選んだうえで、個々のテンソルの変分最適化を行い、最良な表現基底を実装できる点が、TNが本質的に優れた非摂動論的手法といえる所以です。
以上、ファインマン図形とTNのダイヤグラムを対比して紹介してきました。既存のネットワーク構造がおもに経験的に構成されたのに対し、今後は、最適ネットワーク構造の決定原理の解明が重要になると思われます。実際にTTNレベルではエンタングルメントエントロピー最小化原理を使った最適ネットワークの構成アルゴリズムが提案されています。また、ネットワーク=離散系の幾何学です。量子重力との対応という意味においてもTNの構造最適化は鍵になると考えられます。一方で、TN法はファインマン図形のような粒子的描像によるシンプルな物理過程の理解にはあまり向いていません。図2のから延びる脚を眺めてもその意味が直ぐに汲み取れることは稀です。改善のためには、TNダイヤグラムとファインマン図形と関係性の解明は必要と思われますが、まだ系統的な考察は少ないようです。両者とも近似が入らなければ厳密な量子多体系の表現です。その統合的な理解は物理学にとっても重要になるのではないかと予想しています。
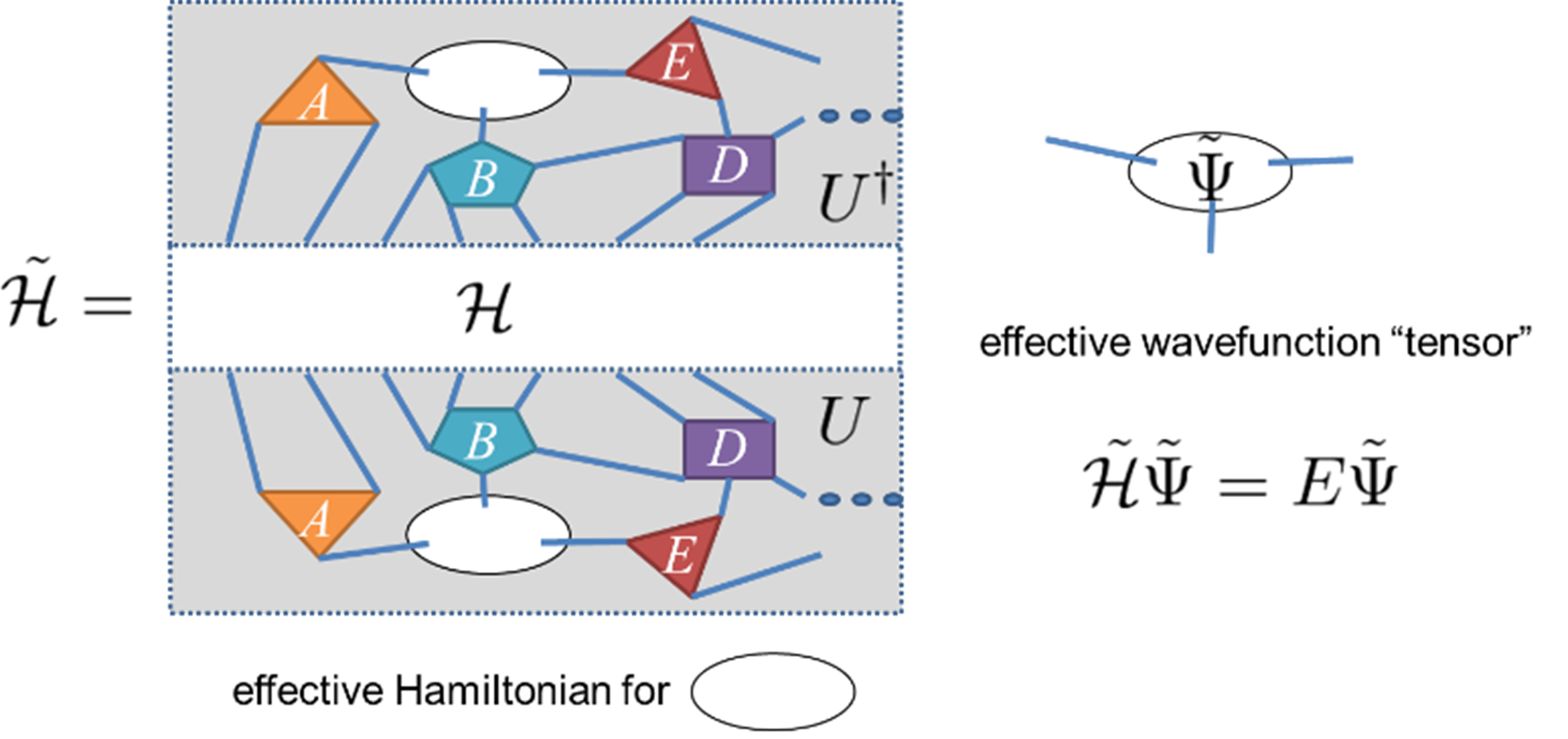
図2:穴あきテンソルネットワークとくりこみらた有効ハミルトニアンの固有値問題
| [1] | 例えばU. Schollwock, Ann. Phys. 326, 96 (2011) K. Okunishi, H. Ueda, T. Nishino, J. Phys. Soc. Jpn.91, 062001 (2022). “Density Matrix and Tensor Network Renormalization” T. Xiang, Cambridge Univ. Press (2023)など。 |
|---|---|
| [2] | 代表的なパッケージとしては、ITensor, TeNPy, TeNeS(国産)などがある。ネットで検索すればよい。 |
| [3] | 初めてTNにダイヤグラムを用いたのは西野、阿久津、筆者らで、1995年頃です。ただし、イジング模型のようにサイト共有型表現だったので広くは流通しませんでした。量子多体系には、辺共有(バーテックス)型表現の方が都合良く、現在はこちらの流儀が一般的です。また、量子多体系分野ではテンソルの脚をくりこまれた補助自由度と解釈しますが、量子情報分野では同じ補助自由度を実効的なベル対と解釈することが多いようです。 |
| [4] | ハバード・ストラトノビッチ変換により有効的な準粒子に書き換えることも多いですが、有効作用の形自体は物理的洞察による決め打ちで、現れる図形も基本的に固定されてしまいます。ただし、準粒子基底は自己無同着に決定するので、(おそらく紫外極限での)変分最適化が入り込んでいます。 |
| [5] | 有限の補助自由度数で求めたスケール次元の精度は、スケール階層性に加えてネットワーク形状の詳細に依存します。例えばHOTRGのようなTTNでは階層性を持ちますが、その指数は古典的です。1+1次元のMERAはそのループ構造によりエンタングルメントエントロピーの対数補正を満たし、臨界現象を正しく 記述できます。 |
